
【题目】已知一副三角板ABE与ACD.
(1)将两个三角板如图(1)放置,连结BD,计算∠1+∠2= .

(2)将图(1)中的三角板BAE绕点A顺时针旋转一个锐角α.
①当α= 时,AB∥CD,如图(2)并计算α+∠1+∠2= .
②当α= 45°时,如图(3),计算α+∠1+∠2= .
③在旋转的过程中,当B点在直线CD的上方时,如图(4), α、∠1、∠2间的数量关系是否会发生变化,为什么?
④当B点运动到直线CD的下方时,如图(5),α(∠CAE)、∠1、∠2间的数量关系是否会发生变化,试说明你的结论?
【答案】 (1)105°;(2)见解析.
【解析】(1)直角三角板一般有两种 ,一种是30°,60°,90° ,另一种是45°,45°,90°.
∴∠BCD=45°+30°=75°
∴∠1+∠2=180°-75°=105°
(2)①连接CE,
若AB∥DC,则∠1+∠2=∠ABE=90°,∴∠BOD=90°
∴∠OCE+∠CEO=180°-∠COE=90°
∴∠ACE+∠AEC=30°+45°+90°=165°
在三角形ACE中,α=180°-165°=15°, α+∠1+∠2=105°
②连接CE
∠EAD+∠ADC=45°+60°=105°, ∴∠DCE+∠AEC=105°
∴∠DCE+∠CEB=105°-45°=60°
∴∠CFE=180°-60°=120°
∴ α+∠1+∠2=180°-120°+45°=105°
③设AC与BE交于点N,BE与CD交于点F
(∠1+∠2)+(∠α+∠C)+∠E=180°,
∠1+∠2+∠α+30°+45°=180°,
∴α+∠1+∠2=105°;
④变化,同上,设AB与DC相交于点F
∠1+(∠α+∠C-∠2)+∠E=180°,
∠1+∠α+30°-∠2+45°=180°,
∴∠α+∠1-∠2=105°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图1,MA1∥NA2 , 则∠A1+∠A2= 度.
如图2,MA1∥NA3 , 则∠A1+∠A2+∠A3= 度.
如图3,MA1∥NA4 , 则∠A1+∠A2+∠A3+∠A4= 度.
如图4,MA1∥NA5 , 则∠A1+∠A2+∠A3+∠A4+∠A5= 度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn , 则∠A1+∠A2+∠A3+…+∠An= 度.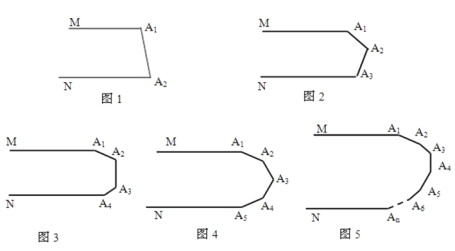
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列作图语句正确的是( )
A. 作射线AB,使AB=a B. 作∠AOB=∠a
C. 延长直线AB到点C,使AC=BC D. 以点O为圆心作弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是严重缺水的国家之一,人均淡水资源为世界人均量的四分之一,所以我们要为中国节水,为世界节水.若每人每天浪费水0.32升,那么100万人每天浪费的水,用科学记数法表示为__________升.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生馅的可能性是否会增大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com