
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
理解:
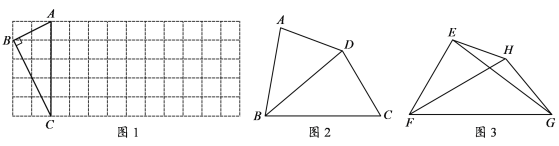
⑴ 如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
⑵ 如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
⑶ 如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为![]() ,求FH 的长.
,求FH 的长.
【答案】(1)如图1,△ACD1、△ACD2、、△ACD3、△ACD4(任画三个即可);(2)BD是四边形ABCD的“相似对角线”,理由见解析;(3)FH=![]() .
.
【解析】
(1)根据“相似对角线”的定义,利用方格纸的特点可找到D点的位置;
(2)先说明∠A+∠ADB=140°=∠ADC,即可说明理由;
(3)先判断出△FEHC∽△FHG,得出FH2=FE·FG,再求出EQ=![]() FE,即可求得FH的值.
FE,即可求得FH的值.
解:(1)由图1可得,AB=![]() ,BC=2
,BC=2![]() ,∠ABC=90°,AC=5,
,∠ABC=90°,AC=5,
四边形ABCD是以AC为“相似对角线”的四边形,
①当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,
∴![]() 或
或![]()
∴CD=10或CD=2.5
同理:当∠CAD=90°时,AD=2.5或AD=10.
根据方格纸的特点可找到D点的位置,然后再连接CD或AD
即如图△ACD1、△ACD2、、△ACD3、△ACD4(任画三个即可)即为所求;

(2)BD是四边形ABCD的“相似对角线”,理由如下:
∵∠ABC=80°,BD平分∠ABC,
∴∠ABD=∠DBC=40°,
∵∠A+∠ADB=140°
∵∠ADC=140°,
∴∠BDC+∠ADB=140°,
∴∠A=∠BDC,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“相似对角线”;
(3)∵FH是四边形EFGH的“相似对角线”,
∴△EFH与△HFG相似,
∵∠EFH=∠HFG,
∴△FEHC∽△FHG,
∴![]()
∴FH2=FE·FG,
如图3,过点E作EQ⊥FG于Q,
∴EQ=FE·sin60°=![]() FE,
FE,
∵![]() .
.
∴![]()
∴FG·FE=24,
∵FH2=FE·FG,
∴FH2=24
∴FH=![]() ,FH=-
,FH=-![]() (舍去)
(舍去)


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,连接BC.
轴交于点C,连接BC.
(1)如图1,求直线BC的表达式;
(2)如图1,点P是抛物线上位于第一象限内的一点,连接PC,PB,当△PCB面积最大时,一动点Q从点P从出发,沿适当路径运动到![]() 轴上的某个点G处,再沿适当路径运动到
轴上的某个点G处,再沿适当路径运动到![]() 轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
(3)如图2,在(2)的条件下,当△PCB面积最大时,把抛物线![]() 向右平移使它的图象经过点P,得到新抛物线
向右平移使它的图象经过点P,得到新抛物线![]() ,在新抛物线
,在新抛物线![]() 上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.
上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
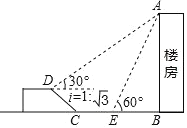
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面![]() 处测得楼房顶部
处测得楼房顶部![]() 的仰角为
的仰角为![]() ,沿坡面向下走到坡脚
,沿坡面向下走到坡脚![]() 处,然后向楼房方向继续行走10米到达
处,然后向楼房方向继续行走10米到达![]() 处,测得楼房顶部
处,测得楼房顶部![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 米,山坡的坡度
米,山坡的坡度![]() (坡度
(坡度![]() 是指坡面的铅直高度与水平宽度的比),求楼房
是指坡面的铅直高度与水平宽度的比),求楼房![]() 高度.(结果精确到0.1米)(参考数据:
高度.(结果精确到0.1米)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF.

(1)求证:四边形AEFD是矩形;(2)若BF=8,DF=4,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
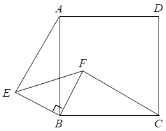
【题目】如图,△EBF为等腰直角三角形,点B为直角顶点, 四边形ABCD是正方形.
⑴ 求证:△ABE≌△CBF;
⑵ CF与AE有什么特殊的位置关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
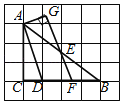
【题目】如图,在网格纸中,每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,点A,B,C,D均落在格点上,点E是AB的中点,过点E作EF∥AD,交BC于点F,作AG⊥EF,交FE延长线于点G,则线段EG的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 2元/公里 |
| 1元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收1元. | |||
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com