
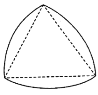
【题目】勒洛三角形是以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形,如图所示,若等边三角形的边长为1,则该勒洛三角形的面积为_____.
【答案】![]()
【解析】
设等边ABC的中心为点O,连接OA,OB,OC,过点O作OD⊥AB于点D,根据锐角三角函数的定义,求出AO,OD的长,从而求出![]() ,进而可得
,进而可得![]() ,根据扇形的面积公式,得
,根据扇形的面积公式,得![]() ,进而可得
,进而可得![]() ,然后即可得到答案.
,然后即可得到答案.
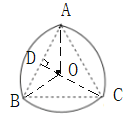
设等边ABC的中心为点O,连接OA,OB,OC,过点O作OD⊥AB于点D,则OA=OB=OC,∠AOB=∠BOC=∠COA=120°,
∵OA=OB,OD⊥AB,
∴∠AOD=![]() ∠AOB=60°, AD=BD=
∠AOB=60°, AD=BD=![]() AB=
AB=![]() ,
,
∵在RtAOD中,sin60°=![]() ,即:
,即: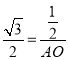 ,
,
∴AO=![]() ,
,
∵在RtAOD中,∠OAD=90°-60°=30°,
∴OD=![]() OA=
OA=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴勒洛三角形的面积=![]() =
=![]() .
.
故答案是:![]() .
.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)( )
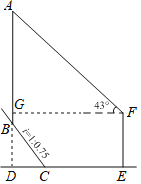
A.46.7mB.46.8mC.53.5mD.67.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和2.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是宝鸡市文化景观标志“天下第一灯”,它由国际![]() 不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分
不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分![]() 层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部
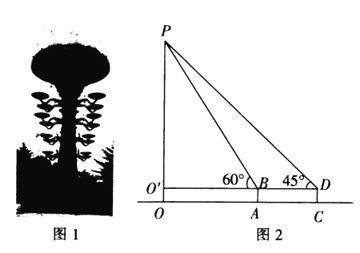
层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部![]() 他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点
他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点![]() 并在点
并在点![]() 处安装了测量器
处安装了测量器![]() 在点
在点![]() 处测得该灯的顶点P的仰角为
处测得该灯的顶点P的仰角为![]() ;再在
;再在![]() 的延长线上确定一点
的延长线上确定一点![]() 使
使![]() 米,在
米,在![]() 点处测得该灯的顶点
点处测得该灯的顶点![]() 的仰角为
的仰角为![]() .若测量过程中测量器的高度始终为
.若测量过程中测量器的高度始终为![]() 米,求“天下第一灯”的高度.
米,求“天下第一灯”的高度.![]() ,最后结果取整数)
,最后结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次“汉字听写”大赛![]() 赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
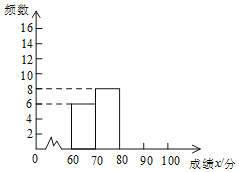
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 请补全频数分布直方图;
请补全频数分布直方图;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m,n 为常数).
(m,n 为常数).
(1)若抛物线的的对称轴为直线 x=1,且经过点(0,-1),求 m,n 的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求 n 的取值范围;
(3)在(1)的条件下,存在正实数 a,b( a<b),当 a≤x≤b 时,恰好有![]() ,请直接写出 a,b 的值.
,请直接写出 a,b 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com