
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9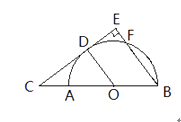
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
【答案】
(1)
解:∵CD切半圆于点D,OD为⊙O的半径,
∴CD⊥OD,
∴∠CDO=90°,
∵BE⊥CD于点E,
∴∠E=90°.
∵∠CDO=∠E=90°,∠C=∠C,
∴△COD∽△CBE.
(2)
解:∵在Rt△BEC中,CE=12,BE=9,
∴CE=15,
∵△COD∽△CBE,
∴![]() ,
,
即![]() ,
,
∴r=![]() .
.
【解析】(1)根据CD切半圆于点D,BE⊥CD于点E,得出∠CDO=∠E=90°,根据三角形两个角对应相等的两个三角形相似得出△COD∽△CBE.
(2)根据(1)中△COD∽△CBE,得出![]() , 从而求出半径。
, 从而求出半径。
【考点精析】利用切线的性质定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
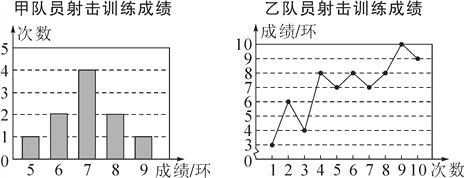
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | 4.2 |
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道。有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最短. 在途中标出M、N的位置,保留画图痕迹;
设方案一中铺设的支管道总长度为L1,方案二中铺设的支管道总长度为L2,则L1与L2的大小关系为:L1_______L2(填“>”、“<”或“=”)理由是____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线 ![]() 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是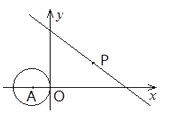
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。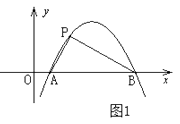

(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。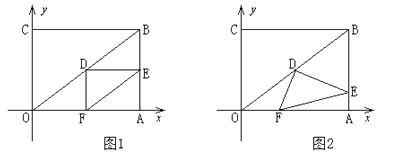
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
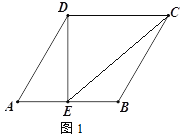
【题目】在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
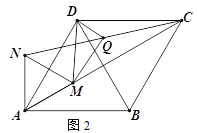
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)在“十一”期间,小明等同学随家长共15人到游乐园游玩,成人门票每张50元,学生门票是6折优惠.他们购票共花了650元,求一共去了几个家长、几个学生?
(2)甲、乙两人骑自行车同时从相距65千米的两地出发相向而行,甲的速度是每小时17.5千米,乙的速度是每小时15千米,求经过几小时甲、乙两人相距32.5千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com