
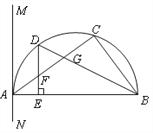
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
【答案】证明见解析
【解析】试题分析:(1)根据圆周角定理推论得到∠ACB=90°,即∠ABC+∠CAB=90°,而∠MAC=∠ABC,则∠MAC+∠BCA=90°,即∠MAB=90°,根据切线的判定即可得到结论;
(2)连AD,根据圆周角定理推论得到∠ABC=90°,由DE⊥AB得到∠DEB=90°,则∠1+∠5=90°,∠3+∠4=90°,又D是弧AC的中点,即弧CD=弧DA,得到∠3=∠5,于是∠1=∠4,利用对顶角相等易得∠1=∠2,则有FD=FG.
试题解析:(1)证明:∵AB为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
而∠MAC=∠ABC,
∴∠MAC+∠CAB=90°,即∠MAB=90°,
∴MN是半圆的切线;
(2)解:如图
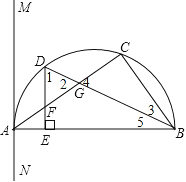
∵AB为直径,
∴∠ACB=90°,
而DE⊥AB,
∴∠DEB=90°,
∴∠1+∠5=90°,∠3+∠4=90°,
∵D是弧AC的中点,即弧CD=弧DA,
∴∠3=∠5,
∴∠1=∠4,
而∠2=∠4,
∴∠1=∠2,
∴FD=FG.


科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【答案】(1)m的值为6;(2)17.
【解析】试题分析:
(1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值;
(2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m的值(此时m的取值需满足根的判别式△![]() ),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
②当7为底边时,则方程的两根相等,由此可得“根的判别式△=0”,从而可得关于m的方程,解方程求得m的值,代入原方程可求得方程的两根,再由三角形三边之间的关系检验即可.
试题解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0时,m≥2,
∴m的值为6;
(2) 若7为腰长,则方程x2-2(m+1)x+m2+5=0的一根为7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
当m=10时,方程x2-22x+105=0,根为x1=15,x2=7,不符合题意,舍去.
当m=4时,方程为x2-10x+21=0,根为x1=3,x2=7,此时周长为7+7+3=17
若7为底边,则方程x2-2(m+1)x+m2+5=0有两等根,
∴Δ=0,解得m=2,此时方程为x2-6x+9=0,根为x1=3,x2=3,3+3<7,不成立,
综上所述,三角形周长为17
点睛:(1)一元二次方程根与系数的关系成立的前提条件是方程要有实数根,即“根的判别式△![]() ”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
【题型】解答题
【结束】
21
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
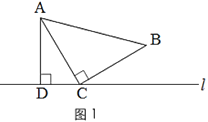
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
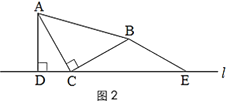
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
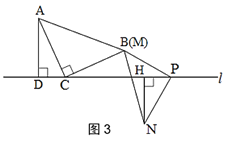
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
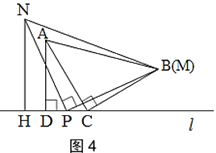
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.

查看答案和解析>>
科目:初中数学 来源: 题型:
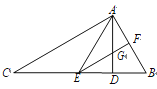
【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
A. 4 个B. 3 个C. 2 个D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com