
���� ��1��������֪[x]��ʾ������x�����������ֱ�ӵó��𰸣�
��2�����Ƚⷽ���飬�ó�[x]��[y]��ֵ�����ó�x��y��ȡֵ��Χ��
��3���ֱ����õ�-1��x��0ʱ����0��x��1ʱ����1��x��2ʱ��[x]=1����x=2ʱ���ֱ�ó�y��ֵ�������ó��𰸣�
��� �⣺��1��������ɵã�[��]=3��[-��]=-4��
�ʴ�Ϊ��3��-4��
��2���ⷽ����ã�$\left\{\begin{array}{l}{[x]=-1}\\{[y]=2}\end{array}\right.$��
��-1��x��0��2��y��3��
��3����-1��x��0ʱ��[x]=-1����ʱy=��-1��2-2����-1��+3=6��
��0��x��1ʱ��[x]=0����ʱy=3��
��1��x��2ʱ��[x]=1����ʱy=12-2��1+3=2��
��x=2ʱ��[x]=2����ʱy=22-2��2+3=3��
����������y���=6��y��С=2��
���� ������Ҫ������ȡ�������Լ���Ԫһ�η�����Ľⷨ�����÷������۵ó�y��ֵ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���BCΪֱ���ġ�O����AB��AC�ڵ�D��E������DE��
��ͼ���ڡ�ABC�У���BCΪֱ���ġ�O����AB��AC�ڵ�D��E������DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
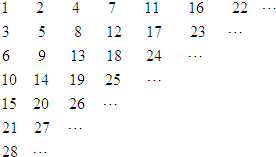
| A�� | 425 | B�� | 426 | C�� | 427 | D�� | 428 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=4��AD=9����E��F�ֱ���BC��AD�ϵĶ��㣬��FECΪ�۽ǣ���ֱ��EF���۾��Σ���C��D�Ķ�Ӧ��ֱ�ΪC�䡢D�䣬��C�䡢D�䡢B��ͬһ��ֱ���ϣ���$\frac{BD��}{BC��}$=$\frac{1}{3}$ʱ����AF�ij�Ϊ3$\frac{5}{6}$��
��ͼ������ABCD�У�AB=4��AD=9����E��F�ֱ���BC��AD�ϵĶ��㣬��FECΪ�۽ǣ���ֱ��EF���۾��Σ���C��D�Ķ�Ӧ��ֱ�ΪC�䡢D�䣬��C�䡢D�䡢B��ͬһ��ֱ���ϣ���$\frac{BD��}{BC��}$=$\frac{1}{3}$ʱ����AF�ij�Ϊ3$\frac{5}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
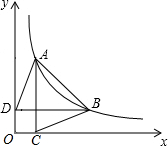 ��ͼ����֪˫����y=$\frac{k}{x}$��x��0��ͼ�������㣬��A��B����ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪC��D������AD��BC����
��ͼ����֪˫����y=$\frac{k}{x}$��x��0��ͼ�������㣬��A��B����ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪC��D������AD��BC�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC=4����BAC=120�㣬��AΪһ������ĵȱ�������ADE�Ƶ�A�ڡ�BAC����ת��AD��AE���ڵ�ֱ����BC�߷ֱ��ڵ�F��G������B����ֱ��AD�ĶԳƵ�ΪB�䣬����FGB�����Ե�GΪֱ�Ƕ����ֱ��������ʱ��BF�ij�Ϊ4$\sqrt{3}$-4��
��ͼ����ABC�У�AB=AC=4����BAC=120�㣬��AΪһ������ĵȱ�������ADE�Ƶ�A�ڡ�BAC����ת��AD��AE���ڵ�ֱ����BC�߷ֱ��ڵ�F��G������B����ֱ��AD�ĶԳƵ�ΪB�䣬����FGB�����Ե�GΪֱ�Ƕ����ֱ��������ʱ��BF�ij�Ϊ4$\sqrt{3}$-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com