
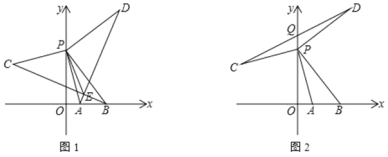
【题目】已知如图,在平面直角坐标系中,点 B(m,0)、A(n,0)分别是 x 轴轴上两点, 且满足多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,点 P(0,h)是 y 轴正半轴上的动点
(1)求三角形△ABP 的面积(用含 h 的代数式表示)
(2)过点 P 作 DP⊥PB,CP⊥PA,且 PD=PB,PC=AP
① 连接 AD、BC 相交于点 E,再连 PE,求∠BEP 的度数
② 连 CD 与 y 轴相交于点 Q,当动点 P 在 y 轴正半轴上运动时,线段 PQ 的长度变不变?如果不变,请求出其值;如果变化,请求出其变化范围
【答案】(1) m=3,n=1; ![]() =h;(2) ∠BEP=135
=h;(2) ∠BEP=135![]() ;(3)PQ=1.
;(3)PQ=1.
【解析】
(1)由多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,可求得m、n的值,可求得三角形△ABP 的面积;
(2)①又DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,可证△BPC≌△DPA,可得∠C=∠A,在CB的线段上取F点,使得CF=AE,连接PF,可得△CPF≌△APE,可得PF=PE, ∠CPF= ∠APE,可得△PEF为等腰直角三角形,可求出∠BEP 的度数;
②由DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,A点坐标为(1,0),B点坐标为(3,0),P点坐标(0,h),由旋转的特性,可得C点坐标为(-h,h-1),D点坐标(h,h+3),
可得CD的解析式,可得Q点坐标及PQ的长.
解:(1) ![]() 多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,
多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,
![]() 展开得:
展开得:![]()
=![]()
![]() m-3=0,
m-3=0,![]() =0,
=0,
解得:m=3,n=1,
![]()
![]() =
=![]() AB
AB![]() OP=
OP=![]()
![]() 2
2![]() h=h;
h=h;
(2)①如图: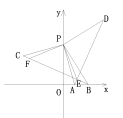
由题意得:DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,
又![]() ∠APB=∠APB,
∠APB=∠APB,![]() ∠APC+∠APB=∠BPD+∠APB
∠APC+∠APB=∠BPD+∠APB
![]() ∠APC=∠BPD,
∠APC=∠BPD,
在△BPC与△DPA中,
PD=PB,PC=AP,∠APC=∠BPD
![]() △BPC≌△DPA,
△BPC≌△DPA,![]() ∠C=∠A
∠C=∠A
在CB的线段上取F点,使得CF=AE,连接PF,
在△CPF与△APE中,
∠C=∠A,CF=AE,PC=AP,
![]() △CPF≌△APE,
△CPF≌△APE,![]() PF=PE, ∠CPF= ∠APE,
PF=PE, ∠CPF= ∠APE,
![]() ∠FPE=90
∠FPE=90![]() ,又PF=PE,
,又PF=PE,
![]() △PEF为等腰直角三角形,
△PEF为等腰直角三角形,
![]() ∠PEF=45
∠PEF=45![]() ,
,
![]() ∠BEP=135
∠BEP=135![]() .
.
②由DP⊥PB,CP⊥PA,且 PD=PB,PC=AP,A点坐标为(1,0),B点坐标为(3,0),P点坐标(0,h),由旋转的特性,可得C点坐标为(-h,h-1),D点坐标(h,h+3),
设CD的解析式为y=kx+b,代入CD两点坐标,可得CD解析式为:![]() ,
,
故Q点坐标为(0,h+1),
![]() P点坐标为(0,h),
P点坐标为(0,h),
![]() PQ的长为定值为:h+1-h=1.
PQ的长为定值为:h+1-h=1.


科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A.当m=﹣3时,函数图象的顶点坐标是( ![]() )
)
B.当m>0时,函数图象截x轴所得的线段长度大于 ![]()
C.当m≠0时,函数图象经过同一个点
D.当m<0时,函数在x ![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在植树节到来之际,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上,O为原点,且BO:OC:CA=2:1:5.
(1)如果点C表示的数是x,请直接写出点A、B表示的数;
(2)如果点A表示的数比点C表示的数两倍还大4,求线段AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
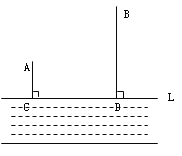
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1=3,则圆O1与圆O2的位置关系是( )
A.相交或相切
B.相切或相离
C.相交或内含
D.相切或内含
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com