
【题目】问题:在1~n(n ≥2)这n个自然数中,每次取两个数(不分顺序),使得所取两数之和大于n,共有多少种取法?
探究:不妨设有m种取法,为了探究m与n的关系,我们先从简单情形入手,再逐次递进,最后猜想得出结论.
探究一:在1~2这2个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于2,有多少种取法?
根据题意,有下列取法:1+2,共1种取法.
所以,当n=2时,m=1.
探究二:在1~3这3个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于3,有多少种取法?
根据题意,有下列取法:1+3,2+3,共2种取法.
所以,当n=3时,m=2.
探究三:在1~4这4个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于4,有多少种取法?
根据题意,有下列取法:1+4,2+4,3+4,2+3,共有3+1=4种取法.
所以,当n=4时,m=3+1=4.
探究四:在1~5这5个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于5,有多少种取法?
根据题意,有下列取法:1+5, 2+5, 3+5, 4+5,2+4,3+4,共有4+2=6种不同的取法.
所以,当n=5时,m=4+2=6.
探究五:在1~6这6个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于6,有多少种不同的取法?(仿照上述探究方法,写出解答过程)
探究六:在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有 种取法?(直接写出结果)
不妨继续探究n=8,9,···时,m与n的关系.
结论:在1~n这n个自然数中,每次取两个数,使得所取的两个数字之和大于n,当n为偶数时,共有___种取法;当n为奇数时,共有___种取法;(只填最简算式)
应用:(1)各边长都是自然数,最大边长为11的不等边三角形共有 个
(2)各边长都是自然数,最大边长为12的三角形共有 个
【答案】探究五:有9种不同的取法,解答过程见解析;
探究六:12;
结论:![]() ,
,![]() ;
;
应用:(1)20;(2)42.
【解析】
探究五和探究六依照上述过程写出即可;
结论:根据n=2~7时,对应m的值,总结规律即可;
应用:(1)相当于求出n=10(偶数)时,对应的m的值,再减去相加等于11的情况;
(2)分两种情况计算:当三角形是不等边三角形时,按(1)同理得出有25个三角形;当三角形是等腰三角形时,再分12为腰和12为底两种情况讨论求解.
探究五:根据题意,有下列取法:1+6,2+6,3+6,4+6,5+6;2+5,3+5,4+5;4+3共有5+3+1=9种取法,所以,当n = 6时,m = 9;
探究六:根据题意,有下列取法:1+7,2+7,3+7,4+7,5+7,6+7;2+6,3+6,4+6,5+6;3+5,4+5;共有6+4+2=12种取法,所以,当n = 7时,m = 12;
结论:根据n=2~7时,对应m的值,可得:当n为偶数时,共有![]() 种取法,当n为奇数时,共有
种取法,当n为奇数时,共有![]() 种取法;
种取法;
应用:(1)∵最大边长为11,
∴设另两边为a、b,a≠b≠11,
∴另两边长可能为:1,2,3,4,5,6,7,8,9,10,
∴a+b>10,共有:![]() =25(个),
=25(个),
∵a+b>11,
∴共有25-5=20(个),
即各边长都是自然数,最大边长为11的不等边三角形共有20个;
(2)最大边长为12,设另两边为a、b,
当三角形是不等边三角形时,则另两边长可能为:1,2,3,4,5,6,7,8,9,10,11,
∴a+b>11,共有:![]() (个),
(个),
∵a+b>12,
∴不等边三角形共有:30-5=25(个),
当三角形是等腰三角形时,①底为12,腰长分别为11,10,9,8,7,一共5个,②腰为12,底为1,2,3,4,5,6,7,8,9,10,11,12,共12个,
综上所述,一共有25+5+12=42(个).


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
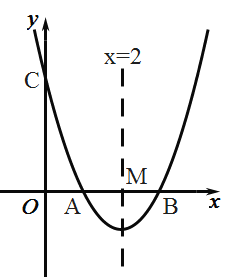
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的函数解析式;
(2)设![]() 为对称轴上一动点,求
为对称轴上一动点,求![]() 周长的最小值;
周长的最小值;
(3)设![]() 为抛物线上一点,
为抛物线上一点,![]() 为对称轴上一点,若以点
为对称轴上一点,若以点![]() 为顶点的四边形是菱形,则点
为顶点的四边形是菱形,则点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为30cm和20cm的矩形铁皮,要在它的四角截去四个边长相等的小正方形,折成一个无盖的长方体盒子,使它的侧面积为272cm2,则截去的正方形的边长是( )cm
A.4cmB.8.5cmC.4cm或8.5cmD.5cm或7.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
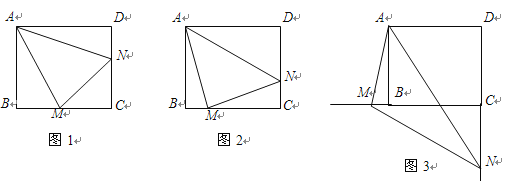
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),求证:
时(如图1),求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),则线段
时(如图2),则线段![]() 和
和![]() 之间数量关系是 ;
之间数量关系是 ;
(3)当![]() 绕点
绕点![]() 旋转到如图3的位置时,猜想线段
旋转到如图3的位置时,猜想线段![]() 和
和![]() 之间又有怎样的的数量关系呢?并对你的猜想加以说明.
之间又有怎样的的数量关系呢?并对你的猜想加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在边长为l的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
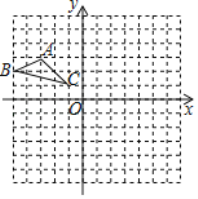
【题目】如图,在边长为![]() 的正方形网格中建立平面直角坐标系,已知
的正方形网格中建立平面直角坐标系,已知![]() 三个顶点分别为
三个顶点分别为![]() ,
,![]() ,
,![]() .
.
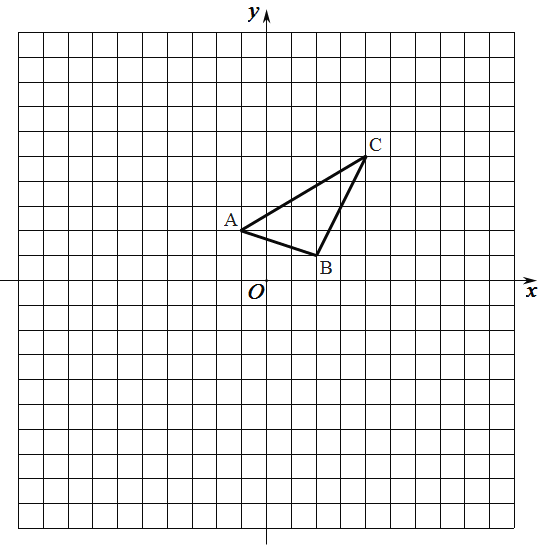
(1)以原点![]() 为位似中心,在
为位似中心,在![]() 轴的上方画出
轴的上方画出![]() ,使
,使![]() 与
与![]() 位似,且相似比为
位似,且相似比为![]() ;
;
(2)![]() 的面积是__________平方单位;
的面积是__________平方单位;
(3)点![]() 为
为![]() 内一点,则在
内一点,则在![]() 内的对应点
内的对应点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
(应用)
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com