
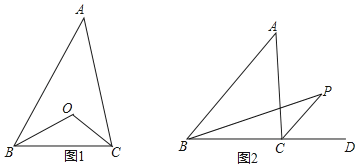
【题目】(1)如图1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度数;
(2)如图2,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,先写出∠A和∠P的数量关系,并证明你的结论.
【答案】(1)∠BOC=118°;(2)∠A=2∠P,理由见解析
【解析】
(1)根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的值;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,根据角平分线的定义可得∠PCD=![]() ∠ACD,∠PBC=
∠ACD,∠PBC=![]() ∠ABC,然后整理得到2∠PCD=∠A.
∠ABC,然后整理得到2∠PCD=∠A.
解:(1)∵∠A=56°,
∴∠ABC+∠ACB=180°-∠A=124°,
∵BO、CO分别是∠ABC和∠ACB的角平分线,
∴∠CBO=∠ABO,∠ACO=∠BCO,
∴∠CBO+∠BCO=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×124°=62°,
×124°=62°,
∴∠BOC=180°-(∠CBO+∠BCO)=118°;
(2)∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABC=2∠PBC,∠ACD=2∠PCD,
∴∠ACD-∠ABC=2(∠PCD-∠PBC),
∵∠A=∠ACD-∠ABC,∠P=∠PCD-∠PBC,
∴∠A=2∠P.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
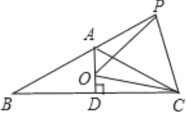
【题目】己知如图,等腰![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是延长线上一点,点
是延长线上一点,点![]() 是线段上一点,
是线段上一点,![]() 下面的结论: ①
下面的结论: ①![]() ;②
;②![]() ;③
;③![]() 是等边三角形④.
是等边三角形④.![]() 其中正确的是( )
其中正确的是( )
A. ①③④B. ①②③C. ①③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分10分)有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你求出摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要绕行
地需要绕行![]() 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成![]() ,
,![]() 两地的直达高铁,可以缩短从
两地的直达高铁,可以缩短从![]() 地到
地到![]() 地的路程.已知:
地的路程.已知:![]() ,
,![]() ,
,![]() 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
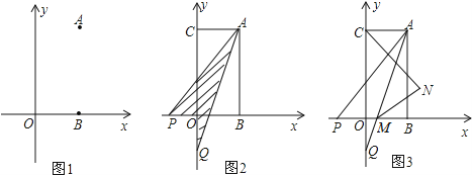
【题目】如图:已知在平面直角坐标系中点A(a,b)点B(a,0),且满足|2a-b|+(b-4)2=0.
(1)求点A、点B的坐标;
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动.同时点Q从C点出发,沿y轴负方向以2个单位每秒的速度移动,某一时刻,如图所示且S阴=![]() S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;
(3)在(2)的条件下,AQ交x轴于M,作∠ACO,∠AMB的角平分线交于点N,判断![]() 是否
是否![]() 为定值,若是定值求其值;若不是定值,说明理由.
为定值,若是定值求其值;若不是定值,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是90分,请问小红在竞赛中答对了多少道题?
(2)小明也参加了竞赛,考完后他说:“这次竞赛我一定能拿到100分.”请问小明有没有可能拿到100分?试用方程的知识来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com