
【题目】学校餐厅中,一张桌子可坐6人,现有以下两种摆放方式:
(1)当有5张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(2)当有n张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(3)新学期有200人在学校就餐,但餐厅只有60张这样的餐桌,若你是老师,你打算选择以下哪种方式来摆放餐桌?为什么?
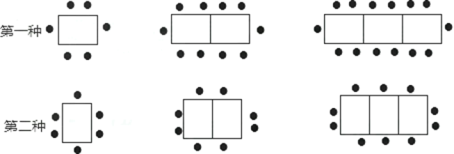
【答案】(1)22,14; ( 2)(2+4n), (4+2n); (3)解: 打算以第一种方式来摆放餐桌,见解析
【解析】
(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人,即有n张桌子时是6+4(n-1)=4n+2;第二种中,有一张桌子时6人,后边多一张桌子多2人,即6+2(n-1)=2n+4,将n=5代入即可得出答案;
(2)根据(1)找出的规律即可得出答案;
(3)分别求出n=60时,两种不同的摆放方式对应的人数,即可得出答案.
解:(1)第一种22人,第二种14人;
(2)第一种(2+4n)人,第二种(4+2n)人;
(3)打算以第一种方式来摆放餐桌
∵第一种中,当n=60时,4×60+2=242>200
第二种中,当n=60时,2×60+4=124<200
∴选择第一种摆放方式.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未成年人思想道德建设越来越受到社会的关注.某青少年研究机构随机调查了某校 100名学生寒假花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查 数据制成了如下的频数分布表(部分空格未填).
某校 100 名学生寒假花零花钱数量的频数分布表:
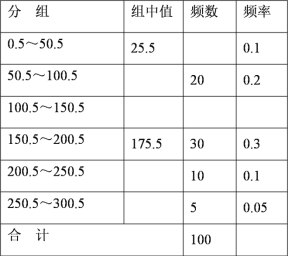
(1)完成该频数分布表;
(2)画出频数分布直方图.
(3)研究认为应对消费 150 元以上的学 生提出勤俭节约的建议.试估计应对该校1200 学生中约多少名学生提出该项建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
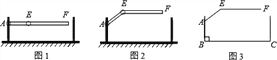
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点![]() 当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示
当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示![]() 栏杆宽度忽略不计
栏杆宽度忽略不计![]() ,其中
,其中![]() 米,那么适合该地下车库的车辆限高标志牌为
米,那么适合该地下车库的车辆限高标志牌为
(参考数据:![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点P是边AB上的一个动点,以每秒3个单位的速度按照从
,若点P是边AB上的一个动点,以每秒3个单位的速度按照从![]() 运动,同时点Q从
运动,同时点Q从![]() 以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若
以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若![]() 为直角三角形,则t的值为________.
为直角三角形,则t的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
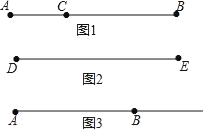
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
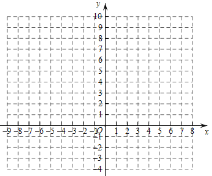
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
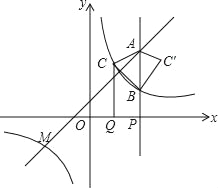
【题目】如图,点M(﹣3,m)是一次函数y=x+1与反比例函数y=![]() (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点.
(1)求反比例函数表达式;
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②当a的值为 时,△AMC与△AMC′的面积相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com