练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．在Rt△ABC中，∠C=90°，AB=10，求sinB=$\frac{2}{5}$，求BC的值．

    分析 根据sinB的值即可求出AC的值，然后利用勾股定理即可求出BC．

    解答 解：∵sinB=$\frac{AC}{AB}$，
    ∴$\frac{AC}{AB}$=$\frac{2}{5}$，
    ∴AC=4，
    ∴由勾股定理即可得：BC=2$\sqrt{21}$，

    点评 本题考查解直角三角形，涉及锐角三角形函数的定义，勾股定理等知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

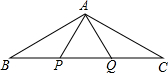    14．已知：点P、Q是△ABC的边BC上的两个点，且BP=PQ=QC=AP=AQ，∠BAC的度数是（　　）
    A．100°B．120°C．130°D．150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

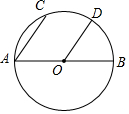    15．如图，AB是⊙O的直径，OD∥AC，C，D两点均在⊙O上，则$\widehat{CD}$与$\widehat{BD}$有何大小关系？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，在⊙O中，$\widehat{AB}$=$\widehat{AC}$，∠B=50°，则∠A=80°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

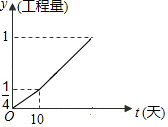    19．甲、乙两工程队完成某项工程，甲先做了10天，然后乙加入合作，完成剩下的工程，设工程总量为1，后期总工程量y与天数t之间的关系为y=kx-$\frac{1}{6}$，若工程进度如图所示，则实际完成这项工程所用的时间比甲单独完成此项工作所用的时间少12天．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．若A•（$\frac{5}{3}$m-n2）=n4-$\frac{25}{9}$m2，则代数式A应是（　　）
    A．-$\frac{5}{3}$m+n2B．-（$\frac{5}{3}$m+n2）C．-n2+$\frac{5}{3}$mD．$\frac{5}{3}$m+n2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

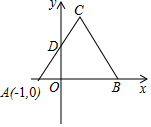    16．已知等边三角形ABC的边长为4，点A的坐标为（一1，0），点B在x轴正半轴上，点C在第一象限，边AC与y轴交于点D．
    （1）求B、C、D三点的坐标．
    （2）求图象经过B、C、D三点的二次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知点C为直线AB上一点，M为AC中点，N为BC中点．

    ①当点C在线段上时，如图，求证：MN=$\frac{1}{2}$AB
    ②当点C在AB的延长线上时或AB的反向延长线上时．画出图形并猜想MN和AB的数最关系，加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算
    （1）（x+1）2-（x+2）（x-2）；
    （2）（a+3）（a-3）（a2-9）．

    查看答案和解析>>

    同步练习册答案