
 (2007•东城区一模)我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.
(2007•东城区一模)我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.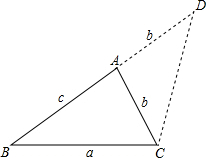
| CD |
| BD |
| AC |
| BC |
| a |
| b+c |
| b |
| a |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2007•东城区一模)如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交AB、BC于点F、E.若AD=2,BC=8.求BE的长.
(2007•东城区一模)如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交AB、BC于点F、E.若AD=2,BC=8.求BE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com