
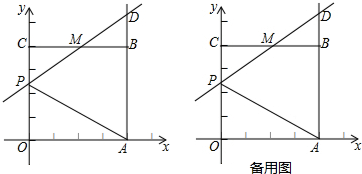
分析 (1)由正方形的性质得出OA=AB=BC=OC=4,∠AOC=∠OCB=90°,证明△DMB∽△PMC,得BD=CP=4-m,AD=8-m,即可得出点D的坐标为;
(2)分两种情况:①当AP=AD时,根据勾股定理得出方程42+m2=(8-m)2,解方程即可;
②当AP=DP时,点P在AD的垂直平分线上,得出OP=$\frac{1}{2}$AD,得出方程m=$\frac{1}{2}$(8-m),解方程即可.
解答 解:(1)∵四边形OABC是正方形,
∴OA=AB=BC=OC=4,∠AOC=∠OCB=90°,
∴∠DBM=90°=∠OCB,
∵M是BC的中点,
∴CM=BM=2,
∵OP=m,
∴CP=4-m,
∵∠PMC=∠DMB,
∴△DMB∽△PMC,
∴$\frac{BD}{CP}=\frac{BM}{CM}$=1,
∴BD=CP=4-m,
∴AD=8-m,
∴点D的坐标为(4,8-m);
(2)分两种情况:①当AP=AD时,
∵AP2=42+m2,
∴42+m2=(8-m)2,
解得:m=3;
②当AP=DP时,点P在AD的垂直平分线上,
∴OP=$\frac{1}{2}$AD,
∴m=$\frac{1}{2}$(8-m),
解得:m=$\frac{8}{3}$;
综上所述:m的值为:3或$\frac{8}{3}$.
点评 本题考查了正方形的性质、坐标与图形性质、勾股定理、相似三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
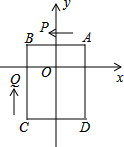 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )| A. | (-1,-1) | B. | (-1,1) | C. | (-2,2) | D. | (1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
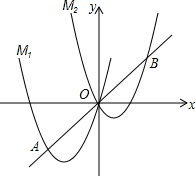 如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.
如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
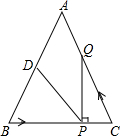 如图,在等腰三角形ABC中,点P、Q分别为线段BC、CA上的动点,点P从点B出发沿BC方向运动,点Q从点C出发沿CA方向运动,两点同时以2cm/s的速度从B、C出发,当P到达C或Q到达A时停止运动,已知D为AB的中点,AB=AC=10cm,BC=8cm,设运动时间为t(s).
如图,在等腰三角形ABC中,点P、Q分别为线段BC、CA上的动点,点P从点B出发沿BC方向运动,点Q从点C出发沿CA方向运动,两点同时以2cm/s的速度从B、C出发,当P到达C或Q到达A时停止运动,已知D为AB的中点,AB=AC=10cm,BC=8cm,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
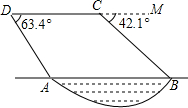 如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.
如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com