Question

1．如图△ABC的顶点坐标分别为A（1，1），B（2，3），C（3，0）．
（1）以点O为位似中心画△DEF，使它与△ABC位似，且相似比为2．
（2）在（1）的条件下，若M（a，b）为△ABC边上的任意一点，则△DEF的边上与点M对应的点M′的坐标为（2a，2b）或（-2a，-2b）．

Answer 1

分析 （1）把点A、B、C的横、纵坐标都乘以2可得到对应点D、E、F的坐标，再描点可得△DEF；把点A、B、C的横、纵坐标都乘以-2可得到对应点D′、E′、F′的坐标，然后描点可得△D′E′F′；
（2）利用以原点为位似中心的位似变换的对应点的坐标特征求解．

解答 解：（1）如图，△DEF和△D′E′F′为所作；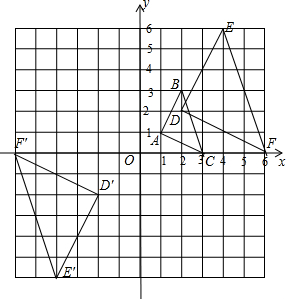

（2）点M对应的点M′的坐标为（2a，2b）或（-2a，-2b）．
故答案为（2a，2b）或（-2a，-2b）．

点评 本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．