
【题目】已知:a、b、c均为非零实数,且a>b>c,关于x的一元二次方程![]() (a≠0)其中一个实数根为2。
(a≠0)其中一个实数根为2。
(1)填空:4a+2b+c 0,a 0,c 0(填“>”,“<”或“=”);
(2)若关于x的一元二次方程![]() (a≠0)的两个实数根,满足一个根为另一个根的2倍,我们就称这样的方程为“倍根方程”,若原方程是倍根方程,则求a、c之间的关系。
(a≠0)的两个实数根,满足一个根为另一个根的2倍,我们就称这样的方程为“倍根方程”,若原方程是倍根方程,则求a、c之间的关系。
(3)若a=1时,设方程的另一根为m(m≠2),在两根之间(不包含两根)的所有整数的绝对值之和是7,求b的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() (形式不唯一);(3)
(形式不唯一);(3)![]() 或
或![]() .
.
【解析】
(1)根据方程的根的定义,把![]() 代入方程,即可得到
代入方程,即可得到![]() 的值,然后利用有理数加减法法则即可判断
的值,然后利用有理数加减法法则即可判断![]() 的符号;
的符号;
(2)根据一元二次方程的根与系数的关系,![]() ,即可求得
,即可求得![]() 的关系;
的关系;
(3)根据一元二次方程的根与系数的关系得:![]() ,当
,当![]() 时,根据
时,根据![]() 在两根之间(不包含两根)的所有整数的绝对值之和是7,确定
在两根之间(不包含两根)的所有整数的绝对值之和是7,确定![]() 的范围,即可得出结论;当
的范围,即可得出结论;当![]() 时,根据
时,根据![]() 在两根之间(不包含两根)的所有整数的绝对值之和是7,确定
在两根之间(不包含两根)的所有整数的绝对值之和是7,确定![]() 的范围,即可得出结论;
的范围,即可得出结论;
解:
(1)把![]() 代入方程
代入方程![]() (a≠0)得:
(a≠0)得:
![]() ,
,
∵![]() 、
、![]() 、
、![]() 均为非零实数,且
均为非零实数,且![]() ,
,
∴若![]() ,则
,则![]() ,
,![]() ,则
,则![]() 不能成立,
不能成立,
同理,![]() ,则
,则![]() ,则
,则![]() 不能成立,
不能成立,
∴![]() ,
,![]() ;
;
(2)根据一元二次方程的根与系数的关系,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() 或
或![]() ;
;
(3)把![]() 代入方程
代入方程![]() (a≠0)得:
(a≠0)得:
![]() ,则
,则![]() ,
,
得:![]() ,
,
∵当![]() 时,2与
时,2与![]() 之间的和为7的整数是3、4,
之间的和为7的整数是3、4,
∴![]() ,
,
得:![]() ,即
,即![]() ;
;
∵当![]() 时,
时,![]() 与2之间的绝对值和为7的整数是1、0、-1、-2、-3,
与2之间的绝对值和为7的整数是1、0、-1、-2、-3,
∴![]() ,
,
得![]() ,则
,则![]() ;
;
故答案为:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
(1)探究![]() 的几何意义:如图①,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,则MO=
的几何意义:如图①,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,则MO=![]() ,因此,
,因此,![]() 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离OM.
的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离OM.
①![]() 的几何意义可以理解为点N1 (填写坐标)与点O(0,0)之间的距离N1O;
的几何意义可以理解为点N1 (填写坐标)与点O(0,0)之间的距离N1O;
②点N2(5,﹣1)与点O(0,0)之间的距离ON2为 .
(2)探究![]() 的几何意义:如图②,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究(1)可知,A′O=
的几何意义:如图②,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究(1)可知,A′O=![]() ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=
,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=![]() ,因此
,因此![]() 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离.
的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离.
(3)探究![]() 的几何意义:请仿照探究二(2)的方法,在图③中画出图形,那么
的几何意义:请仿照探究二(2)的方法,在图③中画出图形,那么![]() 的几何意义可以理解为点C (填写坐标)与点D(x,y)之间的距离.
的几何意义可以理解为点C (填写坐标)与点D(x,y)之间的距离.
(4)拓展应用:①![]()
![]() 的几何意义可以理解为:点A(x,y)与点E(1,﹣4)的距离与点A(x,y)与点F (填写坐标)的距离之和.
的几何意义可以理解为:点A(x,y)与点E(1,﹣4)的距离与点A(x,y)与点F (填写坐标)的距离之和.
②![]() 的最小值为 (直接写出结果)
的最小值为 (直接写出结果)
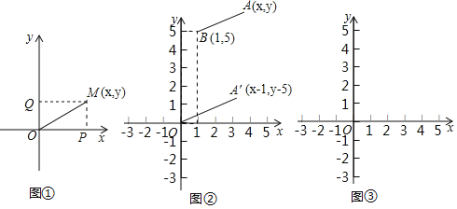
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,点
是等边三角形,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,把
,把![]() 绕着点
绕着点![]() 按逆时针方向旋转,使边
按逆时针方向旋转,使边![]() 与
与![]() 重合,得到
重合,得到![]() ,连接
,连接![]() .求:
.求:![]() 的长及点
的长及点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:


根据以上信息,整理分析数据如下:

(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场计划调整投资策略,对![]() ,
,![]() 两种产品进行市场调查,收集数据如表:
两种产品进行市场调查,收集数据如表:
项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中![]() 是待定常数,其值是由生产
是待定常数,其值是由生产![]() 的材料的市场价格决定的,变化范围是
的材料的市场价格决定的,变化范围是![]() ,销售
,销售![]() 产品时需缴纳
产品时需缴纳![]() 万元的关税,其中
万元的关税,其中![]() 为生产产品的件数,假定所有产品都能在当年售出,设生产
为生产产品的件数,假定所有产品都能在当年售出,设生产![]() ,
,![]() 两种产品的年利润分别为
两种产品的年利润分别为![]() 、
、![]() (万元),写出
(万元),写出![]() 、
、![]() 与
与![]() 之间的函数关系式,注明其自变量
之间的函数关系式,注明其自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要印制期末考试卷,甲印刷厂提出:每套试卷收0.6元印刷费,另收400元制版费;乙印刷厂提出:每套试卷收1元印刷费,不再收取制版费.
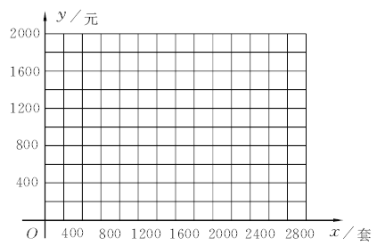
(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;
(2)请在上面的直角坐标系中分别作出(1)中两个函数的图象;
(3)若学校有学生2000人,为保证每个学生均有试卷,则学校至少要付出印刷费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com