
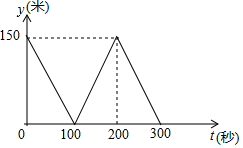
 一次越野跑中,小明和小刚同时出发,当小明跑了1600米时,小刚跑的1400米,此后两人分别以a米/秒、b米/秒的速度匀速跑,他们之间的距离y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1800米.
一次越野跑中,小明和小刚同时出发,当小明跑了1600米时,小刚跑的1400米,此后两人分别以a米/秒、b米/秒的速度匀速跑,他们之间的距离y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为1800米. 分析 由图和题意可知:不妨设此后小明和小刚分别以a米/秒和b米/秒匀速跑,又过100秒时,小刚追上小明,200秒时小刚到达终点,300秒时小明到达终点,由此列出方程组求得a、b,进一步求得答案即可.
解答 解:设此后小明和小刚分别以a米/秒和b米/秒匀速跑,由题意得
$\left\{\begin{array}{l}{1600+100a=1400+100b}\\{1600+300a=1400+200b}\end{array}\right.$解方程组得 $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$.
所以全程=1400+200×2=1800米.
故答案为:1800.
点评 本题考查了函数的图象,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程,就能够通过图象得到函数问题的相应解决.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
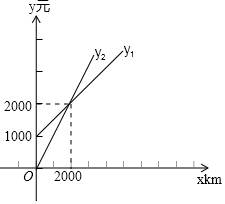 某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com