
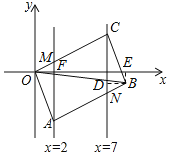
【题目】如图,已知ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为_____.

【答案】9
【解析】
过点B作BD⊥直线x=7,交直线x=7于点D,过点B作BE⊥x轴,交x轴于点E.则OB=![]() .由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
解:过点B作BD⊥直线x=7,交直线x=7于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,
直线x=7与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=7均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中, ,
,
∴△OAF≌△BCD(ASA).
∴BD=OF=2,
∴OE=7+2=9,
∴OB=![]() .
.
∵OE的长不变,
∴当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=9.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】某山是某市民周末休闲爬山的好去处,但总有些市民随手丢垃圾的情况出现.为了美化环境,提高市民的环保意识,某外国语学校某附属学校青年志愿者协会组织50人的青年志愿者团队,在周末前往临某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡130件垃圾.请问该团队的男生和女生各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
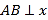
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习概念:
三角形一边的延长线与三角形另一边的夹角叫做三角形的外角.如图1中∠ACD是△AOC的外角,那么∠ACD与∠A、∠O之间有什么关系呢?
∵∠ACD=180°﹣∠ACO,∠A+∠O=180°﹣∠ACO
∴∠ACD=∠A+ ,
结论:三角形的外角等于与它不相邻的两个内角的 .
问题探究:
(1)如图2,已知:∠AOB=∠ACP=∠BDP=60°,且AO=BO,则△AOC △OBD;
(2)如图3,已知∠ACP=∠BDP=45°,且AO=BO,当∠AOB= °,△AOC≌△OBD;
应用结论:

(3)如图4,∠AOB=90°,OA=OB,AC⊥OP,BD⊥OP,请说明:AC=CD+BD.
拓展应用:
(4)如图5,四边形ABCD,AB=BC,BD平分∠ADC,AE∥CD,∠ABC+∠AEB=180°,EB=5,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
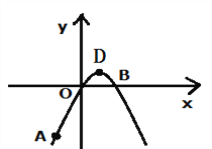
【题目】如图:在平面直角坐标系中,抛物线![]() 经过A(—2,—4 ),O(0,0),B(2,0)三点.
经过A(—2,—4 ),O(0,0),B(2,0)三点.
(1)求抛物线![]() 的解析式和顶点坐标D.
的解析式和顶点坐标D.
(2)若使![]() 轴上一点P,使P 到A、D的距离之和最小,求P的坐标.
轴上一点P,使P 到A、D的距离之和最小,求P的坐标.
(3)若抛物线对称轴上一点M,使AM + OM最小,求AM + OM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com