Question

8．如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）

（1）求B点坐标；
（2）如图2，若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°连OD，求∠AOD的度数；
（3）如图3，过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连FM，等式AM=FM+OF是否成立？若成立，请证明：若不成立，说明理由．

Answer 1

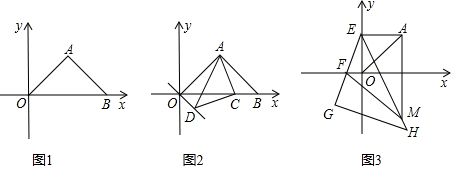
分析 （1）因为△AOB为等腰直角三角形，A（4，4），作AE⊥OB于E，则B点坐标可求；
（2）作AE⊥OB于E，DF⊥OB于F，求证△DFC≌△CEA，再根据等量变换，即可求出∠AOD的度数可求；
（3）在AM上截取AN=OF，连EN，易证△EAN≌△EOF，再根据角与角之间的关系，证明△NEM≌△FEM，则有AM-MF=OF，即可求证等式成立．

解答 解：（1）如图所示，作AE⊥OB于E，
∵A（4，4），
∴OE=4，
∵△AOB为等腰直角三角形，且AE⊥OB，
∴OE=EB=4，
∴OB=8，
∴B（8，0）；

（2）方法一：如图所示，作AE⊥OB于E，DF⊥OB于F，
∵△ACD为等腰直角三角形，
∴AC=DC，∠ACD=90°
即∠ACF+∠DCF=90°，
∵∠FDC+∠DCF=90°，
∴∠ACF=∠FDC，
又∵∠DFC=∠AEC=90°，
∴△DFC≌△CEA（AAS），
∴EC=DF，FC=AE，
∵A（4，4），
∴AE=OE=4，
∴FC=OE，即OF+EF=CE+EF，
∴OF=CE，
∴OF=DF，
∴∠DOF=45°，
∵△AOB为等腰直角三角形，
∴∠AOB=45°，
∴∠AOD=∠AOB+∠DOF=90°；

方法二：如图所示，过C作CK⊥x轴交OA的延长线于K，
则△OCK为等腰直角三角形，OC=CK，∠K=45°，
又∵△ACD为等腰Rt△，
∴∠ACK=90°-∠OCA=∠DCO，AC=DC，
∴△ACK≌△DCO（SAS），
∴∠DOC=∠K=45°，
∴∠AOD=∠AOB+∠DOC=90°；

（3）AM=FM+OF成立，理由：
方法一：如图所示，在AM上截取AN=OF，连EN．
∵A（4，4），
∴AE=OE=4，
又∵∠EAN=∠EOF=90°，AN=OF，
∴△EAN≌△EOF（SAS），
∴∠OEF=∠AEN，EF=EN，
又∵△EGH为等腰直角三角形，
∴∠GEH=45°，即∠OEF+∠OEM=45°，
∴∠AEN+∠OEM=45°
又∵∠AEO=90°，
∴∠NEM=45°=∠FEM，
又∵EM=EM，
∴△NEM≌△FEM（SAS），
∴MN=MF，
∴AM-MF=AM-MN=AN，
∴AM-MF=OF，
即AM=FM+OF；

方法二：如图所示，在x轴的负半轴上截取ON=AM，连EN，MN，
则△EAM≌△EON（SAS），
∴EN=EM，∠NEO=∠MEA，
即∠NEF+∠FEO=∠MEA，
而∠MEA+∠MEO=90°，
∴∠NEF+∠FEO+∠MEO=90°，
而∠FEO+∠MEO=45°，
∴∠NEF=45°=∠MEF，
∴△NEF≌△MEF（SAS），
∴NF=MF，
∴AM=OF=OF+NF=OF+MF，
即AM=FM+OF．

点评 此题属于三角形综合题，主要考查了全等三角形的判定、等腰三角形的性质和坐标与图形性质的综合应用，考核了学生综合运用数学知识的能力．解决问题的关键是根据截长补短的方法，作辅助线构造全等三角形，根据全等三角形的性质进行推导计算．