
【题目】如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.
(1)试说明AH=BH
(2)求证:BD=CG.
(3)探索AE与EF、BF之间的数量关系

【答案】(1)见解析;(2)见解析;(3)AE=EF+BF,理由见解析
【解析】试题分析:
(1)根据等腰三角形的三线合一证明;
(2)证明△ACG≌△CBD,根据全等三角形的性质证明;
(3)证明△ACE≌△CBF即可.
试题解析:
(1)∵AC=BC,CH⊥AB∴AH=BH
(2)∵ABC为等腰直角三角形,且CH⊥AB
∴∠ACG=45°
∵∠CAG+∠ACE=90°,∠BCF+∠ACE=90°
∴∠CAG=∠BCF
在△ACG和△CBD中
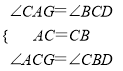
∴△ACG≌△CBD(ASA)
∴BD=CG
(3)AE=EF+BF
理由如下:
在△ACE和△CBF中,
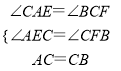
∴△ACE≌△CBF,
∴AE=CF,CE=BF,
∴AE=CF=CE+EF=BF+EF.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】两名同学在调查观众喜欢的影片类型时使用下面提问方式,你认为哪一种更好些( )
A.难道你不认为科幻片比武打片更有意思吗?
B.你更喜欢哪一类电影--科幻片还是武打片?
C.难道你不认为武打片比科幻片更有意思吗?
D.你肯定喜欢科幻片,是吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边.正方形的边长分别是a、b.

(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一: ;方法二: ;
(2)观察图②,试写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 这四个代数式之间的等量关系: ;
这四个代数式之间的等量关系: ;
(3)请利用(2)中等量关系解决问题:已知图①中一个三角形面积是6,图②的大正方形面积是49,求![]() 的值;
的值;
(4)求9972+2×3×997+32的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某汽车销售公司2018年10月份销售一种新型低能耗汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆,求11月份和12月份销量的平均增长率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com