
【题目】如图,四边形![]() 为一个矩形纸片,
为一个矩形纸片,![]() ,
,![]() ,动点
,动点![]() 自
自![]() 点出发沿
点出发沿![]() 方向运动至
方向运动至![]() 点后停止.
点后停止.![]() 以直线
以直线![]() 为轴翻折,点
为轴翻折,点![]() 落到点
落到点![]() 的位置.设
的位置.设![]() ,
,![]() 与原纸片重叠部分的面积为
与原纸片重叠部分的面积为![]() .
.

(1)当![]() 为何值时,直线
为何值时,直线![]() 过点
过点![]() ?
?
(2)当![]() 为何值时,直线
为何值时,直线![]() 过
过![]() 的中点
的中点![]() ?
?
(3)求出![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)当x=![]() 时,直线AD1过点C(2)当x=
时,直线AD1过点C(2)当x=![]() 时,直线AD1过BC的中点E(3)当0<x≤2时,y=x;当2<x≤3时,y=
时,直线AD1过BC的中点E(3)当0<x≤2时,y=x;当2<x≤3时,y=![]()
【解析】
试题分析:(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可;
(2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E=![]() ﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
(3)分为两种情况:当0<x≤2时,y=x;当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,求出AF=PF,作PG⊥AB于G,设PF=AF=a,在Rt△PFG中,由勾股定理得出方程(x﹣a)2+22=a2,求出a即可.
试题解析:
(1)
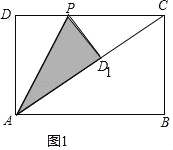
如图1,∵由题意得:△ADP≌△AD1P,
∴AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,
∵直线AD1过C,
∴PD1⊥AC,
在Rt△ABC中,AC=![]() ,CD1=
,CD1=![]() ﹣2,
﹣2,
在Rt△PCD1中,PC2=PD12+CD12,
即(3﹣x)2=x2+(![]() ﹣2)2,
﹣2)2,
解得:x=![]() ,
,
∴当x=![]() 时,直线AD1过点C;
时,直线AD1过点C;
(2)如图2,
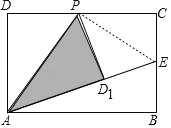
连接PE,
∵E为BC的中点,
∴BE=CE=1,
在Rt△ABE中,AE=![]() =
=![]() ,
,
∵AD1=AD=2,PD=PD1=x,
∴D1E=![]() ﹣2,PC=3﹣x,
﹣2,PC=3﹣x,
在Rt△PD1E和Rt△PCE中,
x2+(![]() ﹣2)2=(3﹣x)2+12,
﹣2)2=(3﹣x)2+12,
解得:x=![]() ,
,
∴当x=![]() 时,直线AD1过BC的中点E;
时,直线AD1过BC的中点E;
(3)如图3,
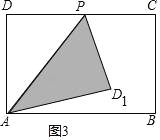
当0<x≤2时,y=x,
如图4,
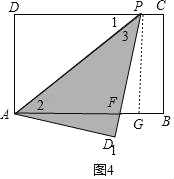
当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,
∵AB∥CD,
∴∠1=∠2,
∵∠1=∠3(根据折叠),
∴∠2=∠3,
∴AF=PF,
作PG⊥AB于G,
设PF=AF=a,
由题意得:AG=DP=x,FG=x﹣a,
在Rt△PFG中,由勾股定理得:(x﹣a)2+22=a2,
解得:a=![]() ,
,
所以y=![]() =
=![]() ,
,
综合上述,当0<x≤2时,y=x;当2<x≤3时,y=![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】海门某公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.求购买该品牌一个台灯、一个手电筒各需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中是假命题的有几个( ).
(1)过一点,有且只有一条直线与已知直线平行.
(2)无理数是开方开不尽的数.
(3)所有有理数都可以用数轴上的点来表示,反过来,数轴上的所有点都表示有理数.
(4)0.01是0.1一个平方根.
A.1个B.3个C.4个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
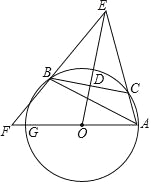
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com