
 如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β
如图,已知△ABC中,∠C=90°,AB=t(t>0),∠A=α,∠B=β 分析 (1)根据sinA=∠A的对边:斜边=$\frac{a}{c}$,cosA=∠A的邻边:斜边=$\frac{b}{c}$,代入相应数据进行计算即可;
(2)根据sinB=∠B的对边:斜边,cosB=∠B的邻边:斜边,代入相应数据进行计算即可.
解答 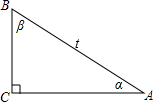 解:(1)∵sinA=$\frac{CB}{AB}$,cosA=$\frac{AC}{AB}$,
解:(1)∵sinA=$\frac{CB}{AB}$,cosA=$\frac{AC}{AB}$,
∴BC=AB×sinA=tsinα,
AC=AB×cosA=tcosα;
(2)∵cosB=$\frac{BC}{AB}$,sinB=$\frac{AC}{AB}$,
∴BC=AB×cosB=tcosβ,
AC=AB×sinB=tsinβ.
点评 此题主要考查了解直角三角形,关键是掌握锐角三角函数的定义.


科目:初中数学 来源: 题型:解答题
 看图填空,如图:
看图填空,如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
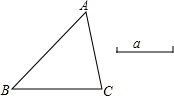 已知△ABC和线段a,且a>$\frac{1}{2}$BC,用直尺和圆规求作⊙O.使⊙O经过B,C两点,且半径为a,并说出可以作出几个圆(要求写出作法).
已知△ABC和线段a,且a>$\frac{1}{2}$BC,用直尺和圆规求作⊙O.使⊙O经过B,C两点,且半径为a,并说出可以作出几个圆(要求写出作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com