
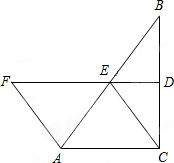
 如图,在△ABC中,∠ACB=90°,FD是线段BC的垂直平分线,交BC于点D,交AB于点E,且AF=CE.
如图,在△ABC中,∠ACB=90°,FD是线段BC的垂直平分线,交BC于点D,交AB于点E,且AF=CE.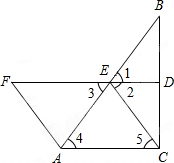 (1)①利用线段垂直平分线的性质得出∠1=∠2=∠3,进而得出∠F=∠3=∠4=∠5,再利用AAS得出全等三角形即可;
(1)①利用线段垂直平分线的性质得出∠1=∠2=∠3,进而得出∠F=∠3=∠4=∠5,再利用AAS得出全等三角形即可;
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| A、6对 | B、5对 | C、4对 | D、3对 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD是矩形,∠1=∠2,∠DEC=90°.
如图,四边形ABCD是矩形,∠1=∠2,∠DEC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
| 4 |
| 9 |
| 2 |
| 3 |
| a4 |
| A、1个 | B、2 个 |
| C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 甲、乙两人骑自行车前往A地,他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示.请根据图象所提供的信息解答下列问题:
甲、乙两人骑自行车前往A地,他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示.请根据图象所提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com