练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
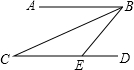
    3．如图，AB∥CD，点E在CD上，BC平分∠ABE，若∠C=25°，则∠BED的度数是（　　）
    A．25°B．45°C．50°D．75°

    分析 由AB∥CD，根据两直线平行，内错角相等，即可求得∠ABC的度数，又由BC平分∠ABE，即可求得∠ABE的度数，继而求得答案．

    解答 解：∵AB∥CD，∠C=25°，
    ∴∠ABC=∠C=25°，
    ∵BC平分∠ABE，
    ∴∠ABE=2∠ABC=50°，
    ∵AB∥CD，
    ∴∠BED=∠ABE=50°．
    故选：C．

    点评 此题考查了平行线的性质，解题时注意：两条平行线被第三条直线所截，内错角相等． 即两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．阅读以下例题：
    解方程|3x|=1
    解：①当3x≥0时，原方程可化为一元一次方程
    3x=1解得x=$\frac{1}{3}$
    ②当3x＜0时，原方程可化为一元一次方程
    -3x=1解得x=-$\frac{1}{3}$
    所以原方程的解是x1=$\frac{1}{3}$，x2=-$\frac{1}{3}$
    仿照以上方法解下列方程：
    （1）|x-3|=2  
    （2）|1-2x|=3-x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

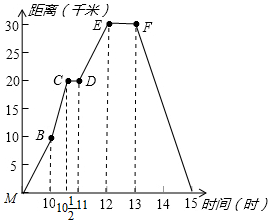    14．如图所示，折线表示小丽骑车离家的距离与时间的关系，小丽上午九时离开家，下午十五时到家，根据折线图所提供的信息，思考并回答下列问题：
    （1）小丽什么时间离家最远？离家最远距离是多少？
    （2）小丽一共休息了几次？各是从什么时间开始的？各休息多少时间？
    （3）小丽什么时刻离家的距离是15千米？（只需回答结果即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．二次函数 y=ax2+bx+2（a≠0）的图象经过点（-1，1），则代数式1-a+b的值为（　　）
    A．-3B．-1C．2D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

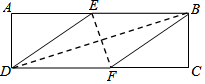    18．在矩形ABCD中，有一个菱形BFDE（点E，F分别在线段AB，CD上），记它们的面积分别为SABCD和SBFDE，现给出下列命题：①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$，则tan∠EDF=$\frac{\sqrt{3}}{3}$；②若DE2=BD•EF，则DF=2AD，则（　　）
    A．①是假命题，②是假命题B．①是真命题，②是假命题
    C．①是假命题，②是真命题D．①是真命题，②是真命题

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：△ABC中，AC=6，BC=8，AB=10，点D是边AB上的一点，过C，D两点的⊙O分别与边CA，CB交于点E，F．

    （1）若点D是AB的中点，
    ①在图1中用尺规作出一个符合条件的图形（保留作图痕迹，不写作法）；
    ②如图2，连结EF，若EF∥AB，求线段EF的长；
    ③请写出求线段EF长度最小值的思路．
    （2）如图3，当点D在边AB上运动时，线段EF长度的最小值是$\frac{24}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列几组数据中，不可以作为直角三角形的三条边的是（　　）
    A．1，2，$\sqrt{3}$B．3，4，5C．1，1，$\sqrt{2}$D．6，12，13

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知a2-4a+1=0，求$\frac{{a}^{8}+1}{{a}^{4}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列图形中既是中心对称图形又是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案