
【题目】国庆假期期间,某单位8名领导和320名员工集体外出进行素质拓展活动,准备租用45座大车或30座小车.若租用2辆大车3辆小车共需租车费1700元;若租用3辆大车2辆小车共需租车费1800元
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名领导,每个人均有座位,且总租车费用不超过3100元,求最省钱的租车方案.
【答案】(1)大车每辆的租车费为400元,小车每辆的租车费为300元;(2)最省钱的租车方案是:6辆大车,2辆小车.
【解析】
(1)设大车每辆的租车费是x元、小车每辆的租车费是y元.根据题意:“租用2辆大车3辆小车共需租车费1700元”;“租用3辆大车2辆小车共需租车费1800元”;列出方程组,求解即可;
(2)根据汽车总数不能小于![]() (取整为8)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(8-m)≤3100,得出取值范围,分析得出即可.
(取整为8)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(8-m)≤3100,得出取值范围,分析得出即可.
(1)设大车每辆的租车费为x元,小车每辆的租车费为y元,
根据题意,得:![]() ,
,
解得:![]() ;
;
答:大车每辆的租车费为400元,小车每辆的租车费为300元;
(2)由每辆汽车上至少要有1名领导,汽车总数不能大于8辆;
又要保证320名员工有车坐,汽车总数不能小于![]() (取整为8)辆,
(取整为8)辆,
综合起来可知汽车总数为8辆.
设租用m辆大型车,则租车费用Q(单位:元)是m的函数,
即Q=400m+300(8﹣m);
化简为:Q=100m+2400,
依题意有:100m+2400≤3100,
∴m≤7,
又要保证320名员工有座位坐,45m+30(8﹣m)≥328,解得m≥![]()
所以有两种租车方案,
方案一:6辆大车,2辆小车;
方案二:7辆大车,1辆小车.
∵Q随m增加而增加,
∴当m=6时,Q最少为3000元.
故最省钱的租车方案是:6辆大车,2辆小车.


科目:初中数学 来源: 题型:
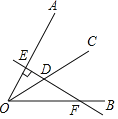
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=1,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是李刚同学在一次测验中解答的数学题:
①若![]() ,则
,则![]() ,
,
②方程![]() 的解为
的解为![]() ,
,
③若![]() 两根的倒数和等于
两根的倒数和等于![]() ,则
,则![]() ,
,
④若![]() 是方程
是方程![]() 的解,则
的解,则![]() 或
或![]() .
.
其中答对的是________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
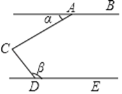
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com