
(2004·海口)在△ABC中,∠ACB=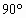 ,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN位于图a所示位置时,求证:
①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN位于图b所示位置时,求证:DE=AD-BE.
(3)当直线MN位于图c所示位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
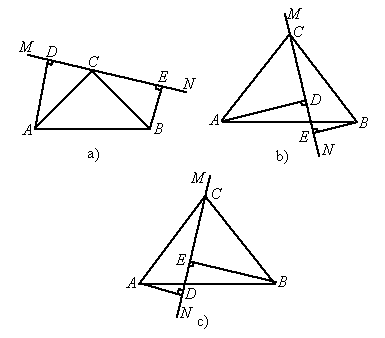
|
解 (1)①因为∠ADC=∠ACB= , ,
所以∠ CAD+∠ACD= . .
∠ BCE+∠ACD=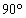 . .
故∠ CAD=∠BCE. 又 AC=BC,∠ADC=∠CEB= , ,
所以△ ADC≌△CEB.②因为△ ADC≌△CEB,所以CE=AD,CD=BE.所以 DE=CE+CD=AD+BE.(2)证明 因为∠ACB=∠CEB= 所以DE=CE-CD=AD-BE. (3)证明 当MN位于图c所示位置时,AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等). 同理证△ACD≌△CBE,得AD=CE,CD=BC,所以DE=CD-CE=BE-AD. |


科目:初中数学 来源: 题型:044
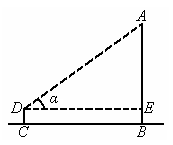
(2004 海口)雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139m的C处(C与塔底B在同一水平线上),用高1.4m的测角仪CD测得塔顶A的仰角α=43°(见图),求这座“千年塔”的高度AB.(结果精确到0.1m)(参考数据:tan43°≈0.9325,cot43°≈1.0724)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com