
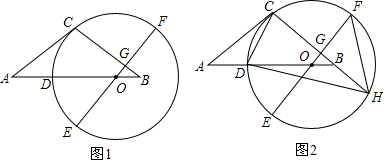
分析 (1)连接OC,根据AC切⊙O于点C得到∠COA+∠A=90°,根据EF⊥BC于点G得到∠GOB=∠CBA=90°,从而得到∠COA=∠GOB=∠DOE,相等的圆心角所对的弧相等得到$\widehat{CD}$=$\widehat{DE}$;
(2)连接OC、CE,由(1)知∠COA=∠DOE,得到∠E+2∠DHC=90°,根据∠E=∠FHC得到∠FHC+2∠DHC=90°,从而证得∠EFH=2∠DHC;
(3)连接OC、OH、CF,根据EF⊥CH得到$\widehat{CF}=\widehat{FH}$,从而得到∠COH=2∠COF,在Rt△COG中,∠CGO=90°,CG=4,得到OG=$\frac{7}{6}$,然后利用勾股定理得到CO,利用勾股定理得到FH=CF=$\sqrt{{3}^{2}+{4}^{2}}$=5.
解答 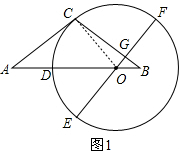 (1)证明:如图1,连接OC,
(1)证明:如图1,连接OC,
∵AC切⊙O于点C,
∴OC⊥AC,
∴∠COA+∠A=90°,
又∵CA=CB,
∴∠A=∠CBA,
∴∠COA+∠CBA=90°,
∵EF⊥BC于点G,
∴∠GOB=∠CBA=90°,
∴∠COA=∠GOB=∠DOE,
∴$\widehat{CD}$=$\widehat{DE}$;
(2)证明:如图2,连接OC、CE,
由(1)知∠COA=∠DOE,
∵OC=OE,
∴CE⊥OD,
∴∠E+∠DOE=90°,
∴∠E+∠DOC=90°,
∵∠DOC=2∠DHC,
∴∠E+2∠DHC=90°,
又∠E=∠FHC,
∴∠FHC+2∠DHC=90°,
∵∠FHC+∠EFH=90°,
∴∠EFH=2∠DHC;
(3)解:如图3,连接OC、OH、CF,
∵EF⊥CH,
∴$\widehat{CF}=\widehat{FH}$,
∴∠COH=2∠COF,
又∵∠COH=2∠CDH,
∴∠COF=∠CDH,
∵CH=8,
∴CG=GH=4,
在Rt△COG中,∠CGO=90°,CG=4,
OG=$\frac{CG}{tan∠COG}$=$\frac{7}{6}$,
∴CO=$\sqrt{{4}^{2}+(\frac{7}{6})^{2}}$=$\frac{25}{6}$,
∴OF=$\frac{25}{6}$,GF=3,
FH=CF=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题考查了圆的综合知识及勾股定理的应用、锐角三角函数的应用等知识,综合性强,难度较大,能够正确的作出辅助线是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
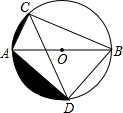 如图,AB为⊙O的直径,弦AC=3,∠ABC=30°,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,弦AC=3,∠ABC=30°,∠ACB的平分线交⊙O于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
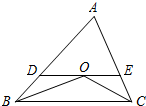 如图,在△ABC中,AB=BC,BO、CO分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交边AB、AC于点D和点E,如果△ABC的周长等于14,△ADE的周长等于9,那么AC=4.
如图,在△ABC中,AB=BC,BO、CO分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交边AB、AC于点D和点E,如果△ABC的周长等于14,△ADE的周长等于9,那么AC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
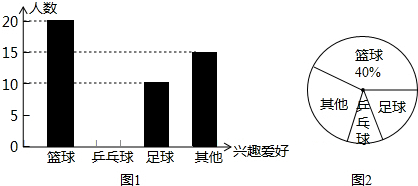
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
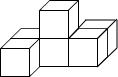 如图所示的几何体是由一些小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )
如图所示的几何体是由一些小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )| A. | 主视图和左视图 | B. | 主视图和俯视图 | ||
| C. | 左视图和俯视图 | D. | 三种视图面积都相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2=2 | B. | x2-(k+1)x+(k+1)=0 | C. | 2x2-$\sqrt{2}$x+1=0 | D. | 1+$\frac{x}{x-1}$=$\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
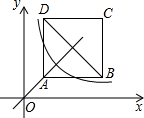 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com