
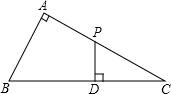
 如图,在△ABC中,∠A=90°,P为AC的中点,PD⊥BC,D为垂足,求证:BD2-CD2=AB2.
如图,在△ABC中,∠A=90°,P为AC的中点,PD⊥BC,D为垂足,求证:BD2-CD2=AB2.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一位运动员在距篮下4m处起跳投篮,恰好投中,球出手时离地面高度为2.25m,球运行的路线是抛物线,已知篮筐中心离地面的距离是3.05m,当球运行的水平距离是2.5m时,球达到最大高度,问球达到最大高度时距离地面多少米?
一位运动员在距篮下4m处起跳投篮,恰好投中,球出手时离地面高度为2.25m,球运行的路线是抛物线,已知篮筐中心离地面的距离是3.05m,当球运行的水平距离是2.5m时,球达到最大高度,问球达到最大高度时距离地面多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
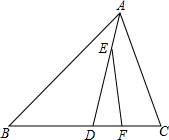 如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°.
如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解刚生产的零件的质量情况,从每一个包装箱内抽5个加以检查 | |
| B. | 为了解全市学生的身高情况,以一、三中的学生为代表进行考察 | |
| C. | 为了解小学生的视力情况,选中六年级20名学生进行调查 | |
| D. | 为了解某地区的车流量,记录某一红绿灯处早上8:00至9:00的车流量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com