
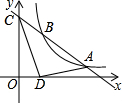
 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.分析 (1)将点A(4,n)和点$B(n+\frac{1}{3},3)$代入y=$\frac{m}{x}$求得m、n的值,即可得出点A、B的坐标,再利用待定系数法求解可得;
(2)先求得直线y=-$\frac{3}{4}$x+4与x轴交点E的坐标,再根据S△ACD=S△CDE-S△ADE求解得出答案.
解答 解:(1)∵点A(4,n)和点$B(n+\frac{1}{3},3)$均在反比例函数y=$\frac{m}{x}$的图象上,
∴$\left\{\begin{array}{l}{4n=m}\\{3(n+\frac{1}{3})=m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=1}\end{array}\right.$,
∴反比例函数的解析式为y=$\frac{4}{x}$,
∴点A(4,1)、B($\frac{4}{3}$,3),
将点A(4,1)、B($\frac{4}{3}$,3)代入y=kx+b,得:
$\left\{\begin{array}{l}{4k+b=1}\\{\frac{4}{3}k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=4}\end{array}\right.$,
∴一次函数的表达式为y=-$\frac{3}{4}$x+4;
(2)设直线y=-$\frac{3}{4}$x+4与x轴交于点E,
则点E的坐标为($\frac{16}{3}$,0),
∴DE=$\frac{16}{3}$-1=$\frac{13}{3}$,
则S△ACD=S△CDE-S△ADE=$\frac{1}{2}$×$\frac{16}{3}$×4-$\frac{1}{2}$×$\frac{13}{3}$×1=$\frac{13}{2}$.
点评 本题考查了用待定系数法求一次函数的解析式和反比例函数的解析式,掌握三角形面积的求法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.

(1)求样本容量,并估计全校同学在周末期间平均每夭做家务活的时间在40分钟以上(含40分钟)的人数;
(2)校学生会拟在表现突出的A、B、C、D四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到A、B两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a-2b+c<0;④2a+b<0;⑤4ac-b2<4a;⑥a+b>0中,其中正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a-2b+c<0;④2a+b<0;⑤4ac-b2<4a;⑥a+b>0中,其中正确的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com