
【题目】如图,在△ABC中,AB=BD,∠BAD=50°,∠C=30°.
(1)求∠BAC的度数;
(2)取AD的中点E,连接BE并延长交AC于点F.求证:AB=BF.

【答案】(1)∠BAC=70°;(2)见解析
【解析】
(1)由等腰三角形的性质求出∠BDA=∠BAD,再由三角形的外角性质得出∠CAD,即可得出∠BAC=∠BAD+∠CAD=70°;
(2)由等腰三角形的性质得出BE⊥AD,求出∠AFE=90°﹣∠CAD=70°,得出∠AFE=∠BAC,即可得出AB=BF.
(1)解:∵AB=BD,
∴∠BDA=∠BAD=50°,
∵∠BDA=∠CAD+∠C,
∴∠CAD=∠BDA﹣∠C=20°,
∴∠BAC=∠BAD+∠CAD=70°;
(2)证明:∵AB=BD,E是AD的中点,
∴BE⊥AD,
∴∠AEF=90°,
∴∠AFE=90°﹣∠CAD=70°,
∴∠AFE=∠BAC,
∴AB=BF.


科目:初中数学 来源: 题型:
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.


(1)求证:BG=DG;
(2)求C′G的长;
(3)如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
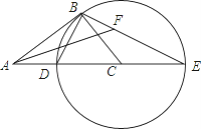
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:![]() ,其中|x|≤1,且x为整数.
,其中|x|≤1,且x为整数.
小海同学的解法如下:
解:原式=![]() ﹣
﹣![]() ①
①
=(x﹣1)2﹣x2+3 ②
=x2﹣2x﹣1﹣x2+3 ③
=﹣2x+2.④
当x=﹣1时,⑤
原式=﹣2×(﹣1)+2⑥
=2+2=4.⑦
请指出他解答过程中的错误(写出相应的序号,多写不给分),并写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成,图中,第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成,…,那么组成第8个黑色L形的正方形个数为( )

A.31B.20C.37D.33
查看答案和解析>>
科目:初中数学 来源: 题型:
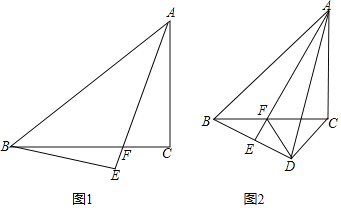
【题目】如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,在△ABE中,∠AEB=90°,AE与BC交于点F.
(1)若∠BAE=30°,BF=2![]() ,求BE的长;
,求BE的长;
(2)如图2,D为BE延长线上一点,连接AD、FD、CD,若AB=AD,∠ACD=135°,求证:BD+BF=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
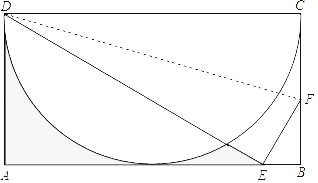
【题目】如图所示,ABCD为矩形,以CD为直径作半圆,矩形的另外三边分别与半圆相切,沿着折痕DF折叠该矩形,使得点C的对应点E落在AB边上,若AD=2,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
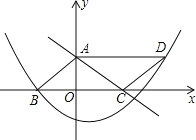
【题目】如图,点A、C分别是一次函数y=﹣![]() x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=
x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=![]() x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
(1)求二次函数的表达式;
(2)动点P从点A到点D,同时动点Q从点C到点A都以每秒1个单位的速度运动,设运动时间为t秒.
①当t为何值时,有PQ丄AC?
②当t为何值时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com