
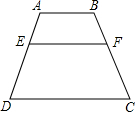
 如图,AB∥EF∥CD.
如图,AB∥EF∥CD.分析 (1)过点A作AN∥BC交CD于N,交EF于M,如图,先判断四边形AMFB、四边形MNCF都为平行四边形得到AB=MF=NC=10,则DN=CD-CN=5,再根据平行线分线段成比例得到$\frac{EM}{DN}$=$\frac{AE}{ED}$=$\frac{2}{3}$,则可计算出EM,然后计算EM+MF即可;
(2)与(1)方法一样得到AB=MF=NC=a,则DN=CD-CN=a-b,再根据平行线分线段成比例得到$\frac{EM}{DN}$=$\frac{AE}{ED}$=k,则EM=kDN=k(a-b),然后计算EM+MF即可.
解答 解:(1)过点A作AN∥BC交CD于N,交EF于M,如图,
∵AB∥EF∥DC,
∴四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=10,
∴DN=CD-CN=15-10=5,
∵EM∥DN,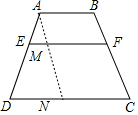
∴$\frac{EM}{DN}$=$\frac{AE}{ED}$=$\frac{2}{3}$,
∴EM=$\frac{2}{3}$×5=$\frac{10}{3}$,
∴EF=EM+MF=$\frac{10}{3}$+10=$\frac{40}{3}$;
(2)∵四边形AMFB、四边形MNCF都为平行四边形,
∴AB=MF=NC=a,
∴DN=CD-CN=a-b,
∵EM∥DN,
∴$\frac{EM}{DN}$=$\frac{AE}{ED}$=k,
∴EM=kDN=k(a-b),
∴EF=EM+MF=k(a-b)+a=(k+1)a-kb.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
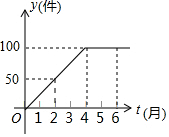 如图是某工厂在2014年前6个月生产某产品的总产量y(件)和时间t(月)的关系的图象,根据图象回答下列问题:
如图是某工厂在2014年前6个月生产某产品的总产量y(件)和时间t(月)的关系的图象,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长.
如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com