
如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn―1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1,A2B1∥A3B2∥A4B3∥…∥AnBn﹣1,△A1A2B1,△A2A3B2,…,△An﹣1AnBn﹣1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为__________;面积小于2014的阴影三角形共有__________个.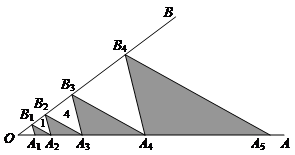
 ;6.
;6.
解析试题分析:根据面积比等于相似比的平方,可得出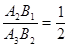 ,
,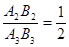 ,再由平行线的性质可得出
,再由平行线的性质可得出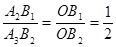 ,
, ,从而可推出相邻两个阴影部分的相似比为1:2,面积比为1:4,先利用等底三角形的面积之比等于高之比可求出第一个及第二个阴影部分的面积,再由相似比为1:2可求出面积小于2011的阴影部分的个数.
,从而可推出相邻两个阴影部分的相似比为1:2,面积比为1:4,先利用等底三角形的面积之比等于高之比可求出第一个及第二个阴影部分的面积,再由相似比为1:2可求出面积小于2011的阴影部分的个数.
试题解析:由题意得,△A2B1B2∽△A3B2B3,
∴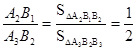 ,
,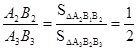 ,
,
又∵A1B1∥A2B2∥A3B3,
∴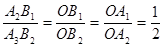 ,
, ,
,
∴OA1=A1A2,B1B2= B2B3
B2B3
继而可得出规律:A1A2= A2A3=
A2A3= A3A4…;B1B2=
A3A4…;B1B2= B2B3=
B2B3= B3B4…
B3B4…
又△A2B1B2,△A3B2B3的面积分别为1、4,
∴S△A1B1A2= ,S△A2B2A3=2,继而可推出S△A3B3A4=8,S△A,4B4A5=32,S△A5B5A6=128,S△A6B6A7=512,S△A7B7A8=2048,
,S△A2B2A3=2,继而可推出S△A3B3A4=8,S△A,4B4A5=32,S△A5B5A6=128,S△A6B6A7=512,S△A7B7A8=2048,
故可得小于2014的阴影三角形的有:△A1B1A2,△A2B2A3,△A3B3A4,△A4B4A5,△A5B5A6,△A6B6A7,共6个.
考点: 1.相似三角形的判定与性质;2.平行线的性质;3.三角形的面积.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:填空题
如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是 .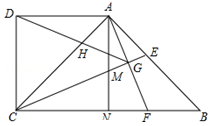
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,已知△ABC是面积为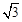 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号)..
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号)..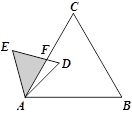
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于
A.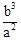 | B.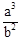 | C.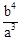 | D.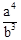 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com