【题目】“牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图、左视图、俯视图依次是（ ）
A.（2）、（4）、（1）B.（3）、（1）、（2）
C.（1）、（4）、（2）D.（3）、（4）、（1）
阶梯计算系列答案科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交
于点F，交过点C的切线于点D．
（1）求证：DC=DP；
（2）若∠CAB=30°，当F是
的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】投石机是古代的大型攻城武器，是数学、工程、物理等复杂学科相互融合的应用（如图（1））．在我国《元史·亦思马因传》中对这种投石机就有过记载（如图（2））．
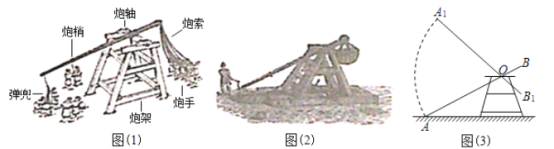
图（3）是图（1）中人工投石机的侧面示意图，炮架的横向支架均与地面相互平行，已知
米，炮轴距地面4.5米，
，炮梢顶端点
能到达水平地面，最高点能到达点
处，且旋转的夹角
（点，，
，
在同一平面内），求点到水平地面的距离．（参考数据：
，
，
，
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝x＋m的图象与反比例函数y＝
的图象交于A，B两点，且与x轴交于点C，点A的坐标为(2，1)．
(1)求m及k的值；
(2)求点C的坐标，并结合图象写出不等式组0＜x＋m≤
的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2020年，新型冠状病毒肆虐全球，疫情期间学生在家进行网课学习和锻炼，学习和身体健康状况都有一定的影响．为了解学生身体健康状况，某校对学生进行立定跳远水平测试．随机抽取50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
| a |
| 12 |
| b |
| 10 |
学生立定跳远测试成绩的频数分布直方图
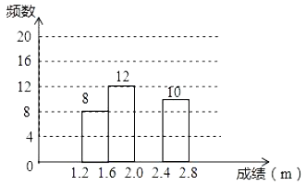
请根据图表中所提供的信息，完成下列问题：
（1）表中
________，
________；
（2）样本成绩的中位数落在________范围内；
（3）请把频数分布直方图补充完整；
（4）该校共有1200名学生，估计该学校学生立定跳远成绩在
范围内的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．
（1）求证：四边形ADEF是平行四边形；
（2）求证：∠DHF=∠DEF．
查看答案和解析>>
科目：初中数学 来源： 题型：
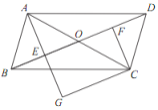
【题目】如图，在□ABCD 中，对角线 AC 与 BD 相交于点 O ，点 E ， F 分别为 OB ， OD 的中点，延长 AE 至 G ，使 EG ＝AE ，连接 CG ．
（1）求证： △ABE≌△CDF ；
（2）当 AB 与 AC 满足什么数量关系时，四边形 EGCF 是矩形？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在近期“抗疫”期间，某药店销售A、B两种型号的口罩，已知销售800只A型和450只B型的利润为210元，销售400只A型和600只B型的利润为180元．
（1）求每只A型口罩和B型口罩的销售利润；
（2）该药店计划一次购进两种型号的口罩共2000只，其中B型口罩的进货量不超过A型口罩的3倍，设购进A型口罩x只，这2000只口罩的销售总利润为y元．
①求y关于x的函数关系式；
②该药店购进A型、B型口罩各多少只，才能使销售总利润最大？
（3）在销售时，该药店开始时将B型口罩提价100%，当收回成本后，为了让利给消费者，决定把B型口罩的售价调整为进价的15%，求B型口罩降价的幅度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
