
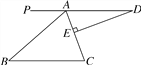
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
【答案】(1)△ABC是等腰三角形,∠B=40°;(2)见解析.
【解析】(1)、根据Rt△ADE的内角和得出∠DAC=70°,根据平行线的性质得出∠C=70°,从而根据有两个角相等的三角形是等腰三角形得出答案;(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线.
解:(1)∵DE⊥AC于点E,∠D=20°,∴∠CAD=70°, ∵AD∥BC,
∴∠C=∠CAD=70°, 又∵∠BAC=70°,∴∠BAC=∠C,∴AB=BC,
∴△ABC是等腰三角形,∴∠B=180°-∠BAC-∠C=180°-70°-70°=40°.
(2)∵延长线段DE恰好过点B,DE⊥AC,∴BD⊥AC,∵△ABC是等腰三角形,
∴DB是∠ABC的平分线.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.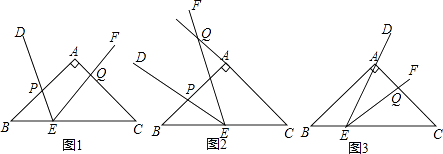
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;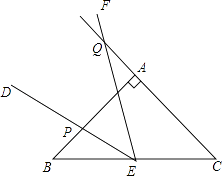
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.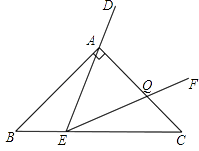
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A.x1=1,x2=﹣1
B.x1=1,x2=2
C.x1=1,x2=0
D.x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月12日植树节活动中,某单位的职工分成两个小组植树,已知他们植树的总数相同,均为100多棵,如果两个小组人数不等,第一组有一人植了6棵,其他每人都植了13棵;第二组有一人植了5棵,其他每人都植了10棵,则该单位共有职工人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题: 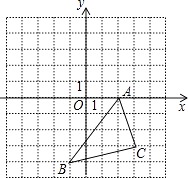
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴张明他们一共去了几个成人,几个学生?
⑵请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?说明理由.
⑶正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
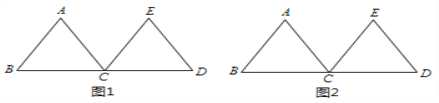
【题目】如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画一个直角三角形; (2)在图2中画出∠ACE的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数分别为_____和_____,p的值为_____.若以C为原点,p的值为_____;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p;
(3)若原点O在图中数轴上点C的右边,且CO=a,求p(用含a的代数式表示).
(4)若原点O在图中数轴上线段BC上,且CO=a,求p(用含a的代数式表示).利用此结果计算当a=0.5时,p的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )
A. 495 B. 497 C. 501 D. 503
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com