
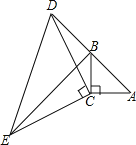
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=2cm,则BE=_______cm.
(3)BE与AD有何位置关系?请说明理由.
【答案】(1)证明见详解;(2)4;(3)BE⊥AD,理由见详解.
【解析】
(1)根据题意,通过SAS即可得证;
(2)由(1)可知BE=AD=2AB;
(3)根据对顶角相等可得∠DCE+∠BEC=∠EBD+∠ADC,由(1)可得∠BEC=∠ADC,则∠EBD=∠DCE=90°.
(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
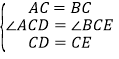 ,
,
∴△ACD≌△BCE(SAS);
(2)∵DB=AB,
∴AD=2AB=4cm,
由(1)得:△ACD≌△BCE,
∴BE=AD=4cm;
故答案为:4;
(3)BE⊥AD;理由如下:
根据对顶角相等得,∠DCE+∠BEC=∠EBD+∠ADC,
由(1)得:△ACD≌△BCE,
∴∠ADC=∠BEC,
∴∠EBD=∠DCE=90°,
∴BE⊥AD.


科目:初中数学 来源: 题型:
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 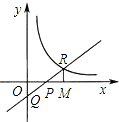
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号) 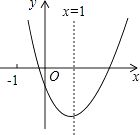
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京东商城销售A、B两种型号的电风扇,销售单价分别为250元、180元,如表是近两周的销售利润情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)

(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= ![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 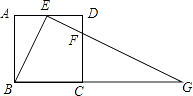
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com