
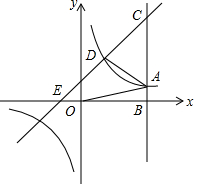
 如图,已知直线BC⊥x轴于点B,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于点A,连接OA,△AOB的面积为1,点A到x轴的距离为$\frac{2}{3}$,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{m}{x}$交于点D(点D的横坐标大于零),并与直线BC交于点C(c,4),与x轴交于点E(-1,0),连接AD.求:
如图,已知直线BC⊥x轴于点B,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于点A,连接OA,△AOB的面积为1,点A到x轴的距离为$\frac{2}{3}$,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{m}{x}$交于点D(点D的横坐标大于零),并与直线BC交于点C(c,4),与x轴交于点E(-1,0),连接AD.求:分析 (1)由AB⊥x轴结合△AOB的面积为1,利用反比例函数系数k的几何意义即可得出m的值,再结合反比例函数图象在第一、三象限即可确定m的值,此题得解;
(2)根据点A的纵坐标结合反比例函数图象上点的坐标特征即可找出点A的坐标,进而即可找出点C的坐标,由点C、E的坐标利用待定系数法即可求出直线CE的解析式,再联立直线CE与反比例函数解析式成方程组,解方程组即可得出点D的坐标;
(3)由点A的坐标可得出点B的坐标,结合点C、E的坐标即可得出BE、BC、AC的长度,再利用分割图形求面积法结合三角形的面积即可求出四边形OADE的面积.
解答 解:(1)∵AB⊥x轴,△AOB的面积为1,
∴S△AOB=$\frac{1}{2}$|m|=1,
∴m=±2,
∵反比例函数的图象在第一、三象限,
∴m=2,
∴反比例函数的解析式为y=$\frac{2}{x}$;
(2)∵点A在反比例函数y=$\frac{2}{x}$的图象上,且点A的纵坐标为$\frac{2}{3}$,
∴点A的坐标为(3,$\frac{2}{3}$),点C的坐标为(3,4).
将点C(3,4)、E(-1,0)代入y=ax+b中,
得:$\left\{\begin{array}{l}{4=3a+b}\\{0=-a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$,
∴直线CE的解析式为y=x+1.
联立直线CE和反比例函数解析式成方程组,
得:$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{2}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-1}\end{array}\right.$,
∵点D的横坐标大于零,
∴点D的坐标为(1,2).
(3)∵点A的坐标为(3,$\frac{2}{3}$),AB⊥x轴于点B,
∴点B的坐标为(3,0),
∴BE=OB+OE=3+1=4.
∵点C的坐标为(3,4),点A的坐标为(3,$\frac{2}{3}$),
∴BC=4,AC=4-$\frac{2}{3}$=$\frac{10}{3}$,
∴S四边形OADE=S△BCE-S△AOB-S△ACD=$\frac{1}{2}$BE•BC-1-$\frac{1}{2}$AC•(xB-xD)=$\frac{1}{2}$×4×4-1-$\frac{1}{2}$×$\frac{10}{3}$×(3-1)=$\frac{11}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数系数k的几何意义、反比例函数图象上点的坐标特征以及三角形的面积,结合图形利用分割图形求面积法求出四边形OADE的面积是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
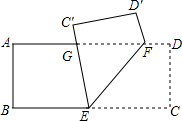 如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,若∠EFG=60°,试求∠BEG的度数.
如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,若∠EFG=60°,试求∠BEG的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
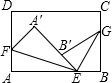 如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?
如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com