
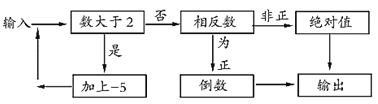
【题目】如图,是一个“有理数转换器”(箭头是数进入转换器的路径,方框是对进入的数进行转换的转化器)
(1)求当小明输入![]() 、
、![]() 两个数时输出的结果;
两个数时输出的结果;
(2)当输出的结果为0时,求输入的数值(写两个即可);
(3)在正数、0、负数中,试探究这个“有理数转化器”不可能输出的数.
【答案】(1)当小明输入![]() 时,输出的结果为
时,输出的结果为![]() ;当小明输入
;当小明输入![]() 时,输出的结果为
时,输出的结果为![]() ;(2)输入的数值是0或5;(注:答案不唯一)(3)在正数、0、负数中,这个“有理数转化器”不可能输出的数是负数.
;(2)输入的数值是0或5;(注:答案不唯一)(3)在正数、0、负数中,这个“有理数转化器”不可能输出的数是负数.
【解析】
(1)根据有理数的大小比较法则、相反数、绝对值运算计算“有理数转换器”即可得;
(2)根据输出结果为0,可推出这个数进入“相反数”和“绝对值”方框时是0,从而可推出进入“数大于2”方框时是0,由此即可得;
(3)根据进入“相反数”方框后,有两个选择,即倒数和绝对值,再根据倒数和绝对值的运算即可得出答案.
(1)![]() ,进入“相反数”方框,结果为3,再进入“倒数”方框,结果为
,进入“相反数”方框,结果为3,再进入“倒数”方框,结果为![]() ,输出
,输出
![]() ,进入“相反数”方框,结果为
,进入“相反数”方框,结果为![]() ,再进入“绝对值”方框,结果为
,再进入“绝对值”方框,结果为![]() ,输出
,输出
故当小明输入![]() 时,输出的结果为
时,输出的结果为![]() ;当小明输入
;当小明输入![]() 时,输出的结果为
时,输出的结果为![]() ;
;
(2)当输入的数值是0时,![]() ,进入“相反数”方框,结果为0,再进入“绝对值”方框,结果为0,输出,符合要求
,进入“相反数”方框,结果为0,再进入“绝对值”方框,结果为0,输出,符合要求
当输入的数值是5时,![]() ,进入“加上
,进入“加上![]() ”方框,结果为0,
”方框,结果为0,![]() ,进入“相反数”方框,结果为0,再进入“绝对值”方框,结果为0,输出,符合要求
,进入“相反数”方框,结果为0,再进入“绝对值”方框,结果为0,输出,符合要求
答:输入的数值是0或5;(注:答案不唯一)
(3)由“有理数转换器”可知,进入“相反数”方框后,有两个选择:①当其为正数时,进入“倒数”方框,输出的结果仍是正数;②当其为非正数(即负数和0)时,进入“绝对值”方框,输出的结果是非负数(即正数和0)
因此,在正数、0、负数中,这个“有理数转化器”不可能输出的数是负数.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
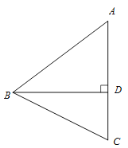
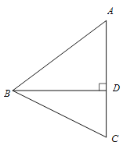
【题目】如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE.
(1)①依题意补全图形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
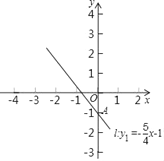
【题目】如图,直线l:y1=﹣![]() x﹣1与y轴交于点A,一次函数y2=
x﹣1与y轴交于点A,一次函数y2=![]() x+3图象与y轴交于点B,与直线l交于点C.
x+3图象与y轴交于点B,与直线l交于点C.
(1)画出一次函数y2=![]() x+3的图象;
x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
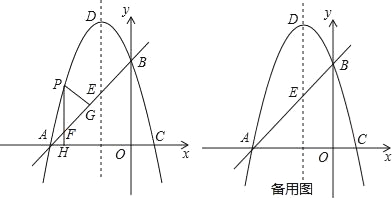
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
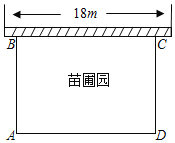
【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“全民阅读”,某校为调查了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成统计图表如下:
学生家庭藏书情况扇形统计图

类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息,解答下列问题:
(1)共抽样调查了______名学生,![]() ______;
______;
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为_______
”对应扇形的圆心角为_______![]() ;
;
(3)若该校有2000名学生,请估计全校学生中家庭藏书超过60本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(-1,0).
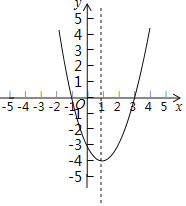
(1)写出B点的坐标 ;
(2)求抛物线的函数解析式;
(3)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(4)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com