练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠2=25°，则∠1的度数为（　　）
    A．20°B．25°C．30°D．35°

    分析 先根据对顶角的定义得出∠3的度数，再由三角形内角和定理求出∠4的度数，根据平行线的性质求出∠ACD的度数，进而可得出结论．

    解答 解：∵∠2=25°，
    ∴∠3=∠2=25°．
    ∵∠A=45°，
    ∴∠4=180°-45°-25°=110°．
    ∵直线l∥m，
    ∴∠ACD=110°，
    ∴∠1=110°-90°=20°．
    故选A．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．统计学校排球队员的年龄，发现有12、13、14、15等四种年龄，统计结果如下表：
    年龄（岁）12131415
    人数（个）2468
    根据表中信息可以判断该排球队员的平均年龄为（　　）
    A．13B．14C．13.5D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

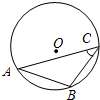    6．如图，点C是⊙O上的动点，弦AB=4，∠C=45°，则S△ABC的最大值是（　　）
    A．$2\sqrt{2}$+4B．8C．$2\sqrt{3}$+4D．4$\sqrt{2}$+4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知Rt△ABC中，AB=AC=$\sqrt{2}$，点D为直线BC上的动点（不与B、C重合），以A为直角顶点作等腰直角三角形ADE（点A，D，E按逆时针顺序排列），连结CE．
    （1）当点D在线段BC上时，
    ①求证：BD=CE；
    ②求CD+CE的值；
    （2）当点D在直线BC上运动时，直接写出CD与CE之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

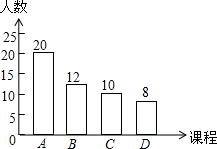    10．某中学计划开设A、B、C、D四门校本课程供学生选修，规定每个学生必须并且只能选修其中一门，为了了解学生的选修意向，现随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的条形统计图，已知该校学生人数为1200人，由此可以估计选修B课程的学生约有288人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．比较大小关系：4＞2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．国家环保局统一规定，空气质量分为5级：1级质量为优；2级质量为良；3级质量为轻度污染；4级质量为中度污染；5级质量为重度污染．某城市随机抽取了一年中某些天的空气质量检测结果，并整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：
    （1）本次调查共抽取了200天的空气质量检测结果进行统计；
    （2）补全条形统计图； 
    （3）扇形统计图中3级空气质量所对应的圆心角为72°； 
    （4）如果空气污染达到中度污染或者以上，将不适宜进行户外活动，根据目前的统计，请你估计该年该城市只有多少天适宜户外活动．（一年天数按365天计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A（2，m）、B（-6，n）两点．则当y1＜y2时，x的取值范围是（　　）
    A．x＞-6或0＜x＜2B．-6＜x＜0或x＞2C．x＜-6或0＜x＜2D．-6＜x＜2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知抛物线y=-$\frac{5}{24}$x2+bx+c分别与x轴、y轴交于点A（-6，0）、B（0，8）．已知点C（4，m）在抛物线上，过点C作CD⊥y轴，垂足为D，AC与y轴交于点E．
    （1）请给出抛物线解析式；
    （2）若令∠BAO=α，请求tan$\frac{α}{2}$的值；（注：要求运用课本所学知识结合题中几何关系进行推导求值）．
    （3）如图2，点P为线段CD上一动点（不与C、D重合），延长PE与x轴交于点M，点N′为AB上点，且∠PMN=∠BAO，若点P横坐标记为x，AN长度记为y，请求出y关于x的函数解析式，并求出AN长度取值范围．

    查看答案和解析>>

    同步练习册答案