练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算：2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$．

    分析 先把各二次根式化为最简二次根式，再合并同类项即可．

    解答 解：原式=$\sqrt{2}$-2$\sqrt{3}$+2$\sqrt{2}$
    =3$\sqrt{2}$-2$\sqrt{3}$．

    点评 本题考查的是二次根式的加减法，熟知二次根式相加减，先把各个二次根式化成最简二次根式，再把被开方数相同的二次根式进行合并，合并方法为系数相加减，根式不变是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．已知一次函数的图象经过点A（2，4），B（-1，-5），C（p，-4）．
    （1）求这个一次函数的解析式；
    （2）求出p的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先仔细阅读材料，再尝试解决问题：
    完全平方公式x2±2xy+y2=（x±y）2及（x±y）2的值恒为非负数的特点在数学学习中有着广泛的应用，比如探求多项式2x2+12x-4的最大（小）值时，我们可以这样处理：
    解：原式=2（x2+6x-2）
    =2（x2+6x+9-9-2）
    =2[（x+3）2-11]
    =2（x+3）2-22
    因为无论x取什么数，都有（x+3）2的值为非负数
    所以（x+3）2的最小值为0，此时x=-3
    进而2（x+3）2-22
    的最小值是2×0-22=-22
    所以当x=-3时，原多项式的最小值是-22
    解决问题：
    请根据上面的解题思路，探求多项式3x2-6x+12的最小值是多少，并写出对应的x的取值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

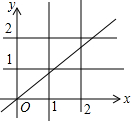    5．如图，若正比例函数y=kx图象与四条直线x=1，x=2，y=1，y=2相交围成的正方形有公共点，则k的取值范围是（　　）
    A．k≤2B．k≥$\frac{1}{2}$C．0＜k＜$\frac{1}{2}$D．$\frac{1}{2}$≤k≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

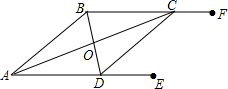    12．如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD，求证：
    （1）AC⊥BD；
    （2）四边形ABCD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列各组数中，不是x+y=7的解是（　　）
    A．$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$B．$\left\{\begin{array}{l}{x=10}\\{y=-3}\end{array}\right.$C．$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$D．$\left\{\begin{array}{l}{x=12}\\{y=-1}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知x2=4，（y+1）3-3=$\frac{3}{8}$，且x＞y，则$\frac{x}{y}$的平方根为±2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列命题是假命题的是（　　）
    A．平分弦的直径垂直于弦
    B．不在同一直线上的三点确定一个圆
    C．矩形的四个顶点在同一个圆上
    D．三角形的内心到三角形三边的距离相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

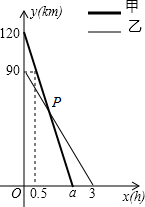    7．在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题：
    （1）A、C两村间的距离为120km，a=2；
    （2）求出甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系式，并求出图中点P的坐标；
    （3）乙在行驶过程中，何时距甲10km？

    查看答案和解析>>

    同步练习册答案