
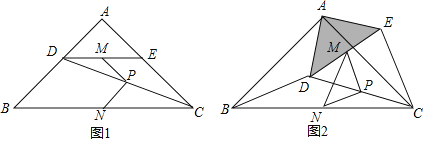
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
【答案】(1)PM=PN, PM⊥PN;(2)△PMN是等腰直角三角形,理由详见解析;(3)![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出结论;
BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)方法1、先判断出MN最大时,△PMN的面积最大,进而求出AN,AM,即可得出MN最大=AM+AN,最后用面积公式即可得出结论.
方法2、先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=14,即可.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN,
(2)由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
同(1)的方法,利用三角形的中位线得,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形,
(3)方法1、如图2,同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大时,△PMN的面积最大,
∴DE∥BC且DE在顶点A上面,
∴MN最大=AM+AN,
连接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=2![]() ,
,
在Rt△ABC中,AB=AC=10,AN=5![]() ,
,
∴MN最大=2![]() +5
+5![]() =7
=7![]() ,
,
∴S△PMN最大=![]() PM2=
PM2=![]() ×
×![]() MN2=
MN2=![]() ×(7
×(7![]() )2=
)2=![]() .
.
方法2、由(2)知,△PMN是等腰直角三角形,PM=PN=![]() BD,
BD,
∴PM最大时,△PMN面积最大,
∴点D在BA的延长线上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=![]() PM2=
PM2=![]() ×72=
×72=![]()


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极绘就我市“一福地、四名城”建设的宏伟蓝图,某镇大力发展旅游业,一店铺专门售卖地方特产“曲山老鹅”,以往销售数据表明,该“曲山老鹅”每天销售数量y(只)与销售单价x(元)满足一次函数y=-![]() x+110,每只“曲山老鹅”各项成本合计为20元/只.
x+110,每只“曲山老鹅”各项成本合计为20元/只.
(1)该店铺“曲山老鹅”销售单价x定为多少时,每天获利最大?最大利润是多少?
(2)该店店主关心教育,决定今后的一段时间从每天的销售利润中捐出200元给当地学校作为本学期优秀学生的奖励资金,为了保证该店捐款后每天剩余利润不低于4000元,试确定该“曲山老鹅”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣6x+8.
(1)将y=x2﹣6x+8化成y=a(x﹣h)2+k的形式;
(2)画出这个二次函数的图象;
(3)当0≤x≤4时,y的取值范围是 .
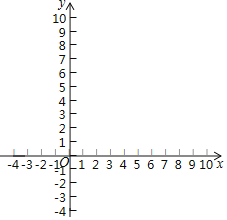
查看答案和解析>>
科目:初中数学 来源: 题型:
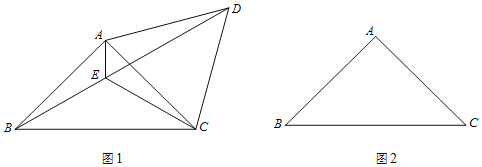
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
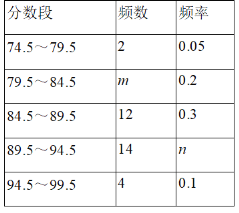
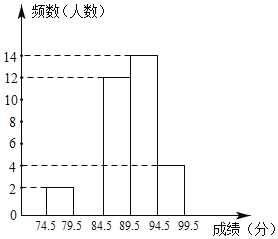
(1)表中m= ,n= ;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正在海岛![]() 西南方向20海里作业的海监船
西南方向20海里作业的海监船![]() ,收到位于其正东方向渔船
,收到位于其正东方向渔船![]() 发出的遇险求救信号,已知渔船
发出的遇险求救信号,已知渔船![]() 位于海岛
位于海岛![]() 的南偏东
的南偏东![]() 方向,海岛
方向,海岛![]() 周围13海里内都有暗礁.(参考数据
周围13海里内都有暗礁.(参考数据![]() ,
,![]() )
)
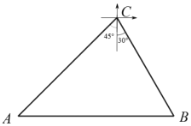
(1)如果海监船![]() 沿正东方向前去救援是否有触礁的危险?
沿正东方向前去救援是否有触礁的危险?
(2)求海监船![]() 与渔船
与渔船![]() 的距离.(结果精确到0.1海里)
的距离.(结果精确到0.1海里)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com