
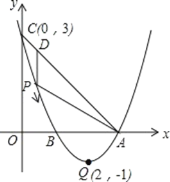
����Ŀ����ͼ����֪������ y=ax2+bx+c��a��0���Ķ�������Ϊ Q��2����1�������� y �ύ�ڵ� C��0��3���� �� x �ύ�� A��B ���㣨�� A �ڵ� B ���Ҳ������� P ���������ϵ�һ���㣬�ӵ� C ���������� �� A �˶����� P �� A ���غϣ������� P �� PD��y �ᣬ�� AC �ڵ� D��
��1����������ߵĺ�����ϵʽ�� A��B ��������ꣻ
��2����� P ���˶��Ĺ����У��߶� PD �����ֵ��
��3������ P ��� Q �غ����� E �� x ���ϣ��� F ���������ϣ����Ƿ������ A��P��E��F Ϊ�� ���ƽ���ı��Σ������ڣ�ֱ��д���� F �����ꣻ�������ڣ���˵��������
���𰸡�(1)y = x - 4x + 3��A (3��0)��B (1��0) ����2�� ![]() ����3��
����3��![]() (
(![]() ��1) ��
��1) ��![]() (
(![]() ��1) ��
��1) ��
��������
��1����֪�����ߵĶ����������ɽ������ߵĽ���ʽ��Ϊ����ʽ��Ȼ����ͼ����C�����������ʽ����������������ߵĽ���ʽ����y=0��������������ɵó�A��B��������
��2���ô���ϵ�������ֱ��AC�Ľ���ʽ����D��x����x+3������P��x��x��4x+3������ʾ��PD�ij������ö��κ��������ʼ��ɽ����
��3������ P ������Ϊ P��2����1���������� Q��ʱ��������������ۣ����� AP Ϊ�߽��й���ƽ���ı��Σ����� AP Ϊ�Խ��߽��й���ƽ���ı�����
��1���������ߵĶ���ΪQ��2����1�������������ߵĽ���ʽΪy=a��x��2��2��1����C��0��3��������ʽ��������3=a��0��2��2��1�������a=1����y=��x��2��2��1����y=x2��4x+3��
��y=0������x2��4x+3=0�������x1=1��x2=3��
�ߵ�A�ڵ�B���ұ�����A��3��0����B��1��0����
��2����ֱ�� AC �ĺ�����ϵʽΪ y=mx+n���� A��3��0����C��0��3��������ʽ�ã�![]() ����ã�
����ã�![]() ����y=��x+3��
����y=��x+3��
��D �� y=��x+3 �ϣ�P �� y=x2��4x+3 �ϣ��� PD��y �ᣬ����D��x����x+3������P��x��x��4x+3������PD=��x+3����x2��4x+3��= ��x2+3x=![]() ���൱ x =
���൱ x = ![]() ʱ��PD ȡ�����ֵΪ
ʱ��PD ȡ�����ֵΪ![]() ��
��
��3������ P ������Ϊ P��2����1���������� Q��ʱ��
���� AP Ϊ�߽��й���ƽ���ı��Σ�ƽ��ֱ�� AP �� x ���ڵ� E������������ F��
��P��2����1��������� F��x��1������x��4x+3=1��![]() =
=![]() ��
��![]() =
=![]() ������������� F ������������ F1��
������������� F ������������ F1��![]() ��1����F2��
��1����F2��![]() ��1����
��1����
���� AP Ϊ�Խ��߽��й���ƽ���ı��Σ������������������ȥ��
�������������������� F ������������ ![]() ��
��![]() ��1����
��1����![]() ��
��![]() ��1����
��1����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�������������ֱ�ΪA��-2��-1����B��-3��-3����C��-1��-3����
��1��������ABC����y��ԳƵ���A1B1C1����д����A1��B1��C1�����ꣻ
��2������A2B2C2������ABCƽ�ƶ��ã��ҵ�A2������Ϊ��-4��4������д��B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
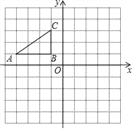
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�������㶼�ڸ���ϣ���A��B��C������ֱ�ΪA����4��1����B����1��1����C����1��3�������������⣺
��1��������ABC����ԭ��O�����ĶԳ�ͼ����A1B1C1����д����C�Ķ�Ӧ��C1�����ꣻ
��2��������ABC��ԭ��O��ʱ����ת90����õ�����A2B2C2����ֱ��д����A��ת��A2������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
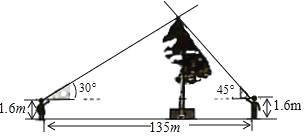
����Ŀ�������ڼ��ڣ�С���С�������ȥ���Σ������ھ��㿴��һ�ù�������С�쾪�ȵ�˵����ѽ���������ߣ���60���ף���С��ȴ����ΪȻ����60���ף��ҿ�û�У������������۲��ݣ��ְ�Ц��˵���������ˣ������Ҵ���һ�����ǰ壬������ѧ����֪ʶ��һ������һ�㣬��˭˵�Ķɣ���
С���С�����������²�������ͼ��ʾ��С���С���ֱ������Ķ�������ͬһ��ƽ���ϣ���������ƽ�����ǰ壬�������ǰ��һ��ֱ�DZ����ƽ��ƽ�У�Ȼ��ǰ���ƶ�����λ�ã�ʹĿ���������ǰ��б�����þ���������ߵ㣬��ʱ�����С���С��֮��ľ���Ϊ135�ף����ǵ��۾�������ľ��붼��1.6�ף�ͨ������˵��С���С��˭��˵����ȷ����������ȷ��0.1�����ο�����![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.24��
��2.24��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ABC����������A��B��C���Եı߷ֱ�Ϊa��b��c����ô���������У������ж���ABC��ֱ�������ε��ǣ�������
A.��A��25������B��65��B.��A����B����C��2��3��5
C.a��b��c��![]() ��
��![]() ��
��![]() D.a��6��b��10��c��12
D.a��6��b��10��c��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��ͼ����ͼ�������н��ۣ���abc��0����a+b+c=2����4a-2b+c��0����b2-4ac��0��������ȷ�Ľ����� ( )
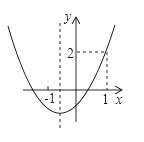
A. �٢� B. �ڢۢ� C. �ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
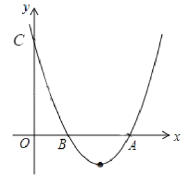
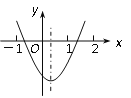
����Ŀ����ͼ��������y��ax2��bx��c�ĶԳ�����![]() ��С��ͨ���۲�ó�������������Ϣ��
��С��ͨ���۲�ó�������������Ϣ��
��c��0����abc��0����a��b��c��0����2a��3b��0.����Ϊ������ȷ����________.������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⲻ��ʽ��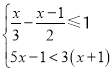 �����������������ĺͣ�
�����������������ĺͣ�
��2���ֽ���ʽ��![]()
��3���ⷽ�̣�![]() ��
��
��4���Ȼ�������ֵ��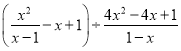 ������
������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
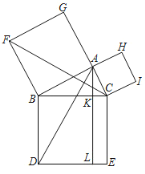
����Ŀ��ŷ������ǹ�ϣ��������ѧ�ҡ�ŷ�ϼ���ѧ�����ߣ�����������ŷ����ù��ɶ���֤����һƬ�Σ�ͬѧ�ǣ�������һ�����߽�ŷ����õ���ѧ�����ɣ�
��֪����Rt��ABC����A=90�����ֱ���AB��AC��BCΪ�������������Σ���ͼ������AD��CF������A��AL��DE�ֱ�BC��DE�ڵ�K��L��
��1����֤����ABD�ա�FBC
��2����֤��������ABFG��������ڳ�����BDLK�����������![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com