
| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 0 |
分析 利用配方法将m=4x2+9y2+12xy+8x+12y+3转化为M=(2x+3y+2)2-1的形式,然后根据非负数的性质来求m的值.
解答 解:m=2x2+9y2+8x-12y+12,
=2(x2+4x+4)+9(y2-$\frac{4}{3}$y+$\frac{4}{9}$),
=2(x+2)2+9(y-$\frac{2}{3}$)2,
∵(x+2)2≥0,(y-$\frac{2}{3}$)2≥0,
∴2(x+2)2+9(y-$\frac{2}{3}$)2≥0,即m≥0,
∴m是非负数.
故选:A.
点评 此题考查了配方法的应用、非负数的性质(偶次方),解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.


科目:初中数学 来源: 题型:解答题
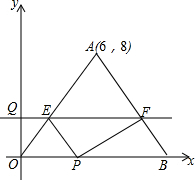 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com