
 ��ƽ��ֱ������ϵ�У��涨��һ������������x�ᷭ�ۣ�������ƽ��2����λ��Ϊһ�α任����֪��ABC������ϵ�е�λ����ͼ��ʾ����ABC����1�α任�õ���A1B1C1��2�˱任��õ���A2B2C2��3�α任��õ���A3B3C3������n�α任��õ���AnBnCn��
��ƽ��ֱ������ϵ�У��涨��һ������������x�ᷭ�ۣ�������ƽ��2����λ��Ϊһ�α任����֪��ABC������ϵ�е�λ����ͼ��ʾ����ABC����1�α任�õ���A1B1C1��2�˱任��õ���A2B2C2��3�α任��õ���A3B3C3������n�α任��õ���AnBnCn������ ��1��������Ŀ������һ�α任�Ĺ��̣��������ζ�Ӧ���λ�ã�Ȼ��˳�����ӣ�
��2����������ͼ�����AA3�ij��ȣ�
��3������A1��A2��A3�����꣬�ҳ����ɣ�д��An�����꣮
��� �⣺��1������ͼ����ͼ��ʾ��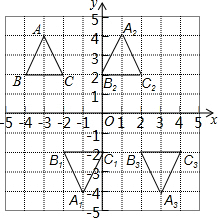 ��
��
��2��AA3=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��3��An��������-3+2n����-1��n4����
���� ���⿼���˸�����ԳƱ任��ͼ�������Ĺؼ��Ƕ������⣬֪��һ�α仯�Ķ��壬��������ṹ������Ӧ���λ�ã�Ȼ��˳�����ӣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��1 | B�� | 1��2 | C�� | 1��1 | D�� | -1��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
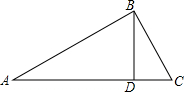 ��ͼ����Rt��ABC�У���ABC=90�㣬BD��AC�ڵ�D����֪tan��CBD=$\frac{1}{2}$��CD=1����AB�ij���
��ͼ����Rt��ABC�У���ABC=90�㣬BD��AC�ڵ�D����֪tan��CBD=$\frac{1}{2}$��CD=1����AB�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ��������ֽ��ABCD��AF�۵�����֪��ADB=25�㣬��ô��BAFΪ����ʱ������ʹAE��BD����ƽ�У�
��ͼ��һ��������ֽ��ABCD��AF�۵�����֪��ADB=25�㣬��ô��BAFΪ����ʱ������ʹAE��BD����ƽ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��?ABCD�У�EG��BC����E��AC�ϣ���G��BD�ϣ���EF��CD��F��GH��AB��H����֤��GH=EF��
��?ABCD�У�EG��BC����E��AC�ϣ���G��BD�ϣ���EF��CD��F��GH��AB��H����֤��GH=EF���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com