
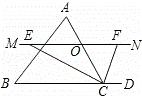
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由.

(1)解:OE=OF.理由如下:
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∵CF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠ECD,
∴∠OFC=∠COF,
∴OF=OC,
∴OE=OF;
(2)△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵当点O运动到 AC的中点时,AO=CO,
AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
(3)解:不可能.
如图所示,
∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=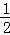 ∠ACB+
∠ACB+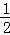 ∠ACD=
∠ACD=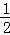 (∠ACB+∠ACD)=90°,
(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.



 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
阅读例题:请参照例题的方法解方程x2﹣|x﹣1|﹣1=0
解方程:x2﹣|x|﹣2=0
解:(1)当x≥0时,得x2﹣x﹣2=0,
解得x1=2,x2=﹣1<0(舍去).
(2 )当x<0时,得x2+x﹣2=0,
)当x<0时,得x2+x﹣2=0,
解得x1=1 (舍去),x2=﹣2.
∴原方程的解为x1=2,x2=﹣2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com