
【题目】如图,正方形ABCD和正方形OPEF中,边AD与边OP重合,![]() ,
,![]() ,点M、N分别在正方形ABCD的边BC、CD上,且
,点M、N分别在正方形ABCD的边BC、CD上,且![]() .将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.
.将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.
(1)请求出t的取值范围;
(2)猜想:正方形OPEF的平移过程中,OE与NM的位置关系.并说明理由.
(3)连结DE、BE.当![]() 的面积等于7时,试求出正方形OPEF的平移时间t的值.
的面积等于7时,试求出正方形OPEF的平移时间t的值.


备用图
【答案】(1)![]() ;(2)OE⊥MN,证明见详解;(3)t的值为:
;(2)OE⊥MN,证明见详解;(3)t的值为:![]() 或
或![]() .
.
【解析】
(1)根据题意,当AD与OP重合时,可求出AF=OF=2,BF=6,然后求出时间的最大值,即可得到t的取值范围;
(2)连接AC,BD,OE,在运动过程中有OE∥AC,由∠CNM=45°=∠CDB,得到BD∥MN,由AC⊥BD,得到AC⊥MN,即可得到OE⊥MN;
(3)由勾股定理求出BD=![]() ,由面积公式,求出△BDE的高为
,由面积公式,求出△BDE的高为![]() ,连接DE,BE,连接OE与BD相交于点H,根据正方形OPEF求出OE的长度,然后得到OH的长度,由等腰三角形△OBH中,根据勾股定理求得OB的长度,然而OB=(8-2t),最后求出t的值.
,连接DE,BE,连接OE与BD相交于点H,根据正方形OPEF求出OE的长度,然后得到OH的长度,由等腰三角形△OBH中,根据勾股定理求得OB的长度,然而OB=(8-2t),最后求出t的值.
(1)根据题意,当AD与OP重合时,
∴![]() ,
,
∴![]() ,
,
当点F到达点B时的时间为:![]() (秒),
(秒),
∴![]() 的取值范围是:
的取值范围是:![]() ;
;
(2)OE与MN是垂直的关系;
如图,连接AC,BD,OE,
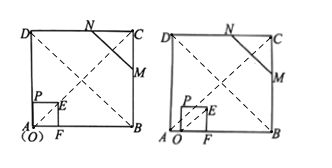
由平移性质得:OE∥AC,
由正方形性质可知,
∵∠CDB=45°=∠CNM
∴MN∥BD,
∵AC⊥BD,
∴AC⊥MN
∴OE⊥MN;
(3)连接DE,BE,连接OE与BD相交于点H,在正方形ABCD中,有AB=AD=8,
∴BD=![]() ,
,
由(2)知,OE⊥BD,则EH是△BDE的高,
由三角形面积公式,得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
① 当点E在BD的下方时,如下图:
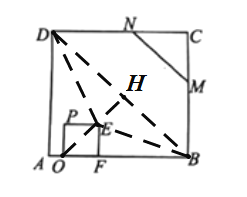
在正方形OPEF中,![]() ,
,
∴![]() ,
,
∵△OBH是等腰直角三角形,OH=BH
∵运动过程中,AO=2t,则OB=(8-2t)
由勾股定理得:![]() ,
,
∴![]() ,
,
解得:![]() ;
;
②当点E在BD的上方时,如图:
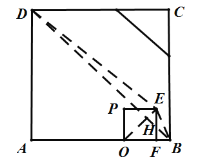
此时,![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∴t的值为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
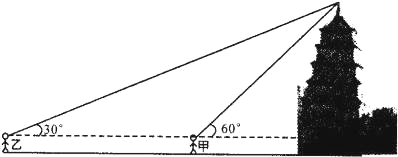
【题目】又到了一年中的春游季节,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.5m;
乙:我们相距20m.
请你根据两位同学的对话,计算白塔的高度.(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
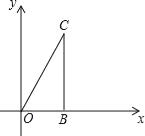
【题目】已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=![]() ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
(2)![]() 的整数部分是______,小数部分是_____;
的整数部分是______,小数部分是_____;
(3)若设![]() 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣![]() y的值.
y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区民用电的计费方式为:白天时段的单价为m元/度,晚间时段的单价为n元/度.某户8月份白天时段用电量比晚间时段多50%,9月份白天时段用电量比8月份白天时段用电量少60%,结果9月份的总用电量虽比8月份的总用电量多20%,但9月份的总电费却比8月份的总电费少10%,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”期间,某商场购进A、B两种品牌的粽子共320袋,其中A品牌比B品牌多80袋.此两种粽子每袋的进价和售价如下表所示,已知销售八袋A品牌的粽子获利136元.(注;利润=售价-进价)
品牌 | A | B |
进价(元/袋) | m | 38 |
售价(元/袋) | 66 | 50 |
(1)试求出m的值.
(2)该商场购进A、B两种品牌的粽子各多少袋?
(3)该商场调整销售策略,A品牌的粽子每袋按原售价销售,B品牌的粽子每袋打折出售.如果购进的A、B两种品牌的粽子全部售出的利润不少于4360元,问B种品牌的粽子每袋最低打几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能用平方差公式计算的是( )
A.(2a+b)(2b﹣a)B.(![]() +1)(﹣
+1)(﹣![]() -1)
-1)
C.(2a﹣3b)(﹣2a+3b)D.(﹣a﹣2b)(﹣a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读某同学解下面分式方程的具体过程.
解方程![]()
解:![]() ①
①
![]() ②
②
![]() ③
③
∴![]() ④
④
∴![]() .
.
把![]() 代入原方程检验知
代入原方程检验知![]() 是原方程的解.
是原方程的解.
请你回答:
(1)得到①式的做法是 ;
得到②式的具体做法是 ;
得到③式的具体做法是 ;
得到④式的根据是 .
(2)上述解答正确吗?如果不正确,从哪一步开始出现错误?答: .错误的原因是 (若第一格回答“正确”的,此空不填).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com