
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 本题有两个等量关系:长×宽=200,长-宽=10,设长为x,宽为y,则可列一元二次方程或二元一次方程组表达本题的等量关系,由此分析各个选项.
解答 解:①设长方形的宽为y,则长为(y+10),所以其面积为:y(y+10)=200,故:选项①正确.
②设长方形的长为x,则宽为(x-10),所以其面积为:x(x-10)=200,故:选项②正确.
③设长方形长为x,宽为y,则由长与宽的关系、长方形的面积公式得$\left\{\begin{array}{l}{x-y=10}\\{xy=200}\end{array}\right.$,故:选项C正确.
④因为长方形的长比宽多10米,则长=宽+10,面积=长×宽,所以$\left\{\begin{array}{l}{x=y+10}\\{xy=200}\end{array}\right.$,故:选项D正确.
故:选D
点评 本题考查了由实际问题抽象出一元二次方程与二元一次方程组、等式的变换等问题,解题的关键是弄清楚题目中隐含的等量关系、设未知数并用未知数表示与之有关系的量.


科目:初中数学 来源: 题型:选择题
 设▲、
设▲、 、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、
、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、 、■这三种物体按质量从大到小排列应为( )
、■这三种物体按质量从大到小排列应为( )| A. | ■、 、▲ 、▲ | B. | ▲、■、 | C. | ■、▲、 | D. |  、▲、■ 、▲、■ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1004 | C. | 2006 | D. | 2007 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
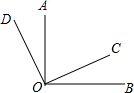 如图所示,∠AOB是直角,∠COD也是直角,∠AOC=65°,那么∠BOD的度数是( )
如图所示,∠AOB是直角,∠COD也是直角,∠AOC=65°,那么∠BOD的度数是( )| A. | 90°+65° | B. | 90°+2×65° | C. | 180°-65° | D. | 180°-2×65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )| A. | 50π-50$\sqrt{3}$ | B. | 50π-25$\sqrt{3}$ | C. | 25π+50$\sqrt{3}$ | D. | 50π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.
在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )| A. | -2.5和-3之间 | B. | -3和-3.5之间 | C. | -3.5和-4之间 | D. | -4和-4.5 之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 肯定没有同一个班级的学生 | |
| B. | 可能有两名同学在一班级,但可能很小 | |
| C. | 至少有三名学生在同一个班级 | |
| D. | 至少有两名学生在同一个班级 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com