Question

有下列说法：①四个角都相等的四边形是矩形；②有一组对边平行，有两个角为直角的四边形是矩形；③两组对边分别相等且有一个角为直角的四边形是矩形；④对角线相等且有一个角是直角的四边形是矩形；⑤对角线互相平分且相等的四边形是矩形；⑥一组对边平行，另一组对边相等且有一角为直角的四边形是矩形．其中，正确的个数是

1. A.
   2个
2. B.
   3个
3. C.
   4个
4. D.
   5个

Answer 1

C
分析：根据四边形的内角和定理求出∠A=∠B=∠C=∠D=90°，即可判断①；根据直角梯形的定义和矩形的判定即可判断②；得出平行四边形，根据矩形的判定判断③即可；根据矩形的判定判断④即可；根据平行四边形的判定和矩形的判定判断⑤即可；根据平行线推出AB是两平行线间的高，推出CD也是平行线间的高，进行判断即可．
解答：
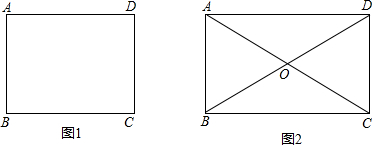
如图1，∠A=∠B=∠C=∠D=360°÷4=90°，∴①正确；
如图1AD∥BC，∠A=∠B=90°，不能推出∠C和∠D也是90°，如直角梯形，∴②错误；
∵AD=BC，AB=CD，
∴四边形ABCD是平行四边形，
∵∠A=90°，
∴平行四边形ABCD是矩形，∴③正确；
根据对角线相等和有一个角是直角不能推出四边形是平行四边形，即不是矩形，∴④错误；
∵OA=OC，OB=OD，
∴四边形ABCD是平行四边形，
∵AC=BD，
∴平行四边形ABCD是矩形，∴⑤正确；
∵AD∥BC，∠A=90°，
∴∠B=90°，
即AB是两平行线AD和BC间的高，
∵CD=AB，
∴CD应也是AD和BC间的高，
∴CD⊥BC，
根据矩形的定义得出四边形是矩形，∴⑥正确；
∴正确的个数是4个，
故选C．
点评：本题综合考查了平行四边形、矩形、直角梯形的判定等知识点的应用，关键是检查学生能否熟练地运用定理进行说理，题型较好，但是一道容易出错的题目．