
【题目】如图,正方形ABCD的边长为4厘米,动点P从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿拆线BC-CD以2厘米/秒的速度匀速移动。点P、Q同时出发,当点P停止运动,点Q也随之停止。联结AQ交BD于点E。设点P运动时间为t秒。
(1)用t表示线段PB的长;
(2)当点Q在线段BC上运动时,t为何值时,∠BEP和∠BEQ相等;
(3)当t为何值时,线段P、Q之间的距离为2![]() cm.
cm.

【答案】(1)PB=4-t;(2)t=![]() ;(3)t=2或
;(3)t=2或![]() ;
;
【解析】
(1)根据正方形的性质和已知条件即可求解;(2)由正方形的性质得出∠PBE=∠QBE,再证明△BEP≌△BEQ,根据全等三角形的性质可得BP=BQ,即可得出方程4-t=2t,解方程即可求得t值;(3)分两种情况讨论:①当![]() 时和②当
时和②当![]() 时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
(1)PB=AB-AP,
∵AB=4,AP=1×t=t,
∴PB=4-t.
(2)当t=![]() 时,∠BEP和∠BEQ相等,理由如下:
时,∠BEP和∠BEQ相等,理由如下:
∵四边形ABCD正方形,
∴ 对角线BD平分∠ABC,
∴∠PBE=∠QBE,
当∠BEP=∠BEQ 时,
在△BEP和△BEQ中,
 ,
,
∴△BEP≌△BEQ,
∴BP=BQ,
即4-t=2t,
解得t=![]() ;
;
(3)分两种情况讨论:
①当![]() 时,即当P点在AB上,Q点在BC上运动时,
时,即当P点在AB上,Q点在BC上运动时,
连接PQ,如图1所示:

根据勾股定理得:![]() ,
,
即![]()
解得t=2或t=![]() (负值舍去);
(负值舍去);
②当![]() 时,即当P点在AB上,Q点在CD上运动时,
时,即当P点在AB上,Q点在CD上运动时,
作PM⊥CD于M,如图2所示:
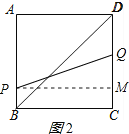
∴PM=BC=4,CM=BP=4-t,MQ=2t-4-(4-t)=3t-8,
根据勾股定理得:![]() ,
,
即![]()
解得t=2(舍去)或t=![]() ;
;
综上,当t=2或t=![]() 时,PQ之间的距离为2
时,PQ之间的距离为2![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图,对正方形纸片ABCD进行如下操作: 
(i)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=α1;
(ii)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=α2;
(iii)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=α3;
按此作法从操作(2)起重复以上步骤,得到α1 , α2 , …,αn , …,现有如下结论:①当α1=10°时,α2=40°;②2α4+α3=90°; ③当α5=30°时,△CDE9≌△ADE10;④当α1=45°时,BE2= ![]() .
.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y= ![]() 图像恰好过点D,则k的值为( )
图像恰好过点D,则k的值为( )
A.6
B.﹣6
C.9
D.﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的![]() ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.
(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3![]() ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: 
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙两段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
图中的数字表示每一级台阶的高度(单位:cm),并且数据15,16,16,14,14,15的方差s甲2=![]() ,数据11,15,18,17,10,19的方差s乙2=
,数据11,15,18,17,10,19的方差s乙2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.
(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时 ![]() +
+ ![]() 的值;
的值;
②试说明无论k取何值, ![]() +
+ ![]() 的值都等于同一个常数.
的值都等于同一个常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AOB中,∠AOB=90°,AO=6厘米,BO=8厘米,分别以OB和OA所在直线为x轴,y轴建立平面直角坐标系,如图所示,动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动,同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动(其中一点到达终点时,另一点随即停止移动).
(1)求过点A和点B的直线表达式;
(2)当点M移动多长时间时,四边形AMNB的面积最小?并求出四边形AMNB面积的最小值;
(3)在点M和点N移动的过程中,是否存在以O,M,N为顶点的三角形与△AOB相似?若存在,请求出点M 和点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com