
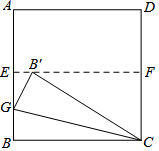
 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度. 分析 由对折得出CB=CB′,在Rt△B′FC中,sin∠CB′F=$\frac{CF}{CB′}$=$\frac{1}{2}$,得出∠CB′F=30°,根据EF∥BC,得到∠B′CB=∠CB′F=2∠GCB′=30°,于是得到结论;
解答 解:如图1,由对折可知,∠EFC=90°,CF=$\frac{1}{2}$CD,
∵四边形ABCD是正方形,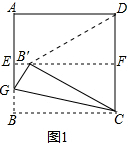
∴CD=CB,
∴CF=$\frac{1}{2}$BC,
∵CB′=CB,
∴CF=$\frac{1}{2}$CB′
∴在Rt△B′FC中,sin∠CB′F=$\frac{CF}{CB′}$=$\frac{1}{2}$,
∴∠CB′F=30°,
∵EF∥BC,
∴∠BCB′=CB′F=30°,
∴∠GCB′=$\frac{1}{2}$∠BCB′=15°,
∴∠B′GC=90°-15°=75°
故答案为75;
点评 本题考查翻折变换、正方形的性质、特殊角的三角函数等知识,解决本题的关键是找准对折后的相等角,相等边,求出∠CB′F=30°,是本题的突破点,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
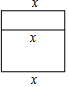 用20米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )
用20米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )| A. | x(20-x)平方米 | B. | x(10-x)平方米 | C. | $x({10-\frac{3}{2}x})$平方米 | D. | $x({\frac{20-2x}{3}})$平方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 96×105 | B. | 960×104 | C. | 9.6×107 | D. | 9.6×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
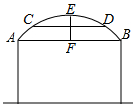 某村想在村口建一个牌门,村长根据往来车辆的高度、宽度画了图纸如图,交给小张制作.小张看到图纸很困惑,因为他发现牌门的下部分是矩形,而上部分不知是圆弧还是抛物线形状.图纸上只标明了跨度AB为4米,最高处点E到AB的距离EF为1米,与AB平行的横梁CD到AB的距离FG为0.5米,CD为3米.请你能帮小张解决困惑,写出解题过程.
某村想在村口建一个牌门,村长根据往来车辆的高度、宽度画了图纸如图,交给小张制作.小张看到图纸很困惑,因为他发现牌门的下部分是矩形,而上部分不知是圆弧还是抛物线形状.图纸上只标明了跨度AB为4米,最高处点E到AB的距离EF为1米,与AB平行的横梁CD到AB的距离FG为0.5米,CD为3米.请你能帮小张解决困惑,写出解题过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
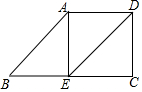 如图,已知在四边形中ABCD,AD∥BC,过点A作AE⊥BC于点E,连接DE,∠BAE=46°,且△ABE≌△EDA.
如图,已知在四边形中ABCD,AD∥BC,过点A作AE⊥BC于点E,连接DE,∠BAE=46°,且△ABE≌△EDA.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
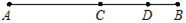 如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长3.
如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com