
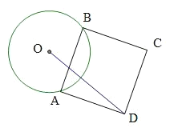
【题目】如图,⊙O 的半径为 3,AB 为圆上一动弦,以 AB 为边作正方形 ABCD,求 OD 的最大值__.
【答案】3![]() +3
+3
【解析】
把AO绕点A顺时针旋转90![]() 得到AO′,得到△AOO′是等腰直角三角形,根据等腰直角三角形的性质求出OO′,再根据正方形的性质可得AB=AD,再求出∠BAO=∠DAO′,然后利用“边角边”证明△ABO和△ADO′全等,根据全等三角形对应边相等可得DO′=BO,再根据三角形的任意两边之和大于第三边求解即可.
得到AO′,得到△AOO′是等腰直角三角形,根据等腰直角三角形的性质求出OO′,再根据正方形的性质可得AB=AD,再求出∠BAO=∠DAO′,然后利用“边角边”证明△ABO和△ADO′全等,根据全等三角形对应边相等可得DO′=BO,再根据三角形的任意两边之和大于第三边求解即可.
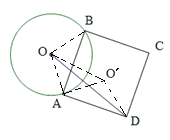
如图,连接AO、BO、把AO绕点A顺时针旋转90![]() 得到AO′,连接DO’
得到AO′,连接DO’
∴△AOO′是等腰直角三角形,
∵AO=3,
∴OO′=![]() =3
=3![]() ,
,
在正方形ABCD中,AB=AD,∠BAD=90![]() ,
,
∵∠BAO+∠BAO′=∠DAO′+∠BAO′=90![]() ,
,
∴∠BAO=∠DAO′,
在△ABO和△ADO′,
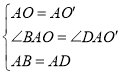 ,
,
∴△ABO≌△ADO′(SAS),
∴DO′=BO=3,
∴OO′+O′D≥OD,
当O、O′、D三点共线时,取“=”,
此时,OD的最大值为3![]() +3.
+3.
故答案为:3![]() +3.
+3.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有三张卡片,三张卡片的正面分别标有数字![]() ,
,![]() ,
,![]() ,这些卡片除数字外都相同,将卡片搅匀.
,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数卡片的概率是_________.
(2)先从盒子中任意抽取一张卡片,再从余下的两张卡片中任意抽取一张卡片,求抽取的两张卡片标有数字之和大于![]() 的概率(请用画树状图或列表等方法求解).
的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,以点A为圆心AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
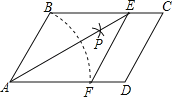
(1)求证:四边形ABEF是菱形;
(2)若∠C=60°,AE=4![]() ,求菱形ABEF的面积.
,求菱形ABEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
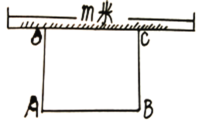
【题目】为配合我市“创建全国文明城市”某单位计划在一块矩形空地上修建绿色植物园(如图所示),其中边靠墙(墙长为![]() 米),另外三边用总长36米的材料围成.若
米),另外三边用总长36米的材料围成.若![]() 米,矩形
米,矩形![]() 的面积为
的面积为![]() 平方米.
平方米.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若矩形面积为160平方米,求![]() 的长.
的长.
(3)在(2)的前提下,墙长![]() 米对
米对![]() 的长有影响吗?请详细说明.
的长有影响吗?请详细说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点;
为抛物线顶点;
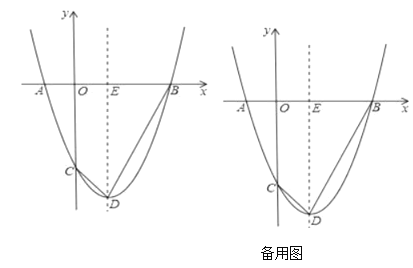
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)连结![]() 、
、![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.
①若线段![]() 上有一点
上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
②若抛物线上一点![]() ,作
,作![]() ,交直线
,交直线![]() 于点
于点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
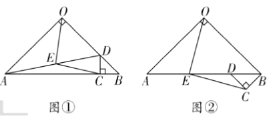
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com