
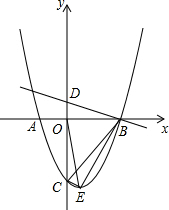
 已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C.对称轴为x=1,顶点为E,直线y=-$\frac{1}{3}$x+1交y轴于点D.
已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C.对称轴为x=1,顶点为E,直线y=-$\frac{1}{3}$x+1交y轴于点D.分析 (1)在抛物线y=ax2-2x+c中,已知对称轴x=-$\frac{b}{2a}$=1,可求出a的值;再将点A的坐标代入抛物线的解析式中,可确定c的值,由此得解.
(2)首先由抛物线的解析式,确定点B、C、E的坐标,由直线BD的解析式能得到点D的坐标;在求出△BCE、△BOD的三边长后,由SSS来判定这两个三角形相似.
(3)△BOE的面积易得,而在(2)中求出了BD的长,由△BDP、△BOE的面积相等先求出点P到直线BD的距离,如何由这个距离求出点P的坐标?这里需要进行适当的转化;首先在y轴上取一点(可设为点M),使得点M到直线BD的距离等于点P到直线BD的距离,通过解直角三角形先求出DM的长,由此确定点M的坐标,然后过M作平行于直线BD的直线,再联立抛物线的解析式即可确定点P的坐标.
解答 解:(1)抛物线y=ax2-2x+c中,对称轴x=-$\frac{b}{2a}$=-$\frac{-2}{2a}$=1,∴a=1;
将点A(-1,0)代入y=ax2-2x+c中,得:1+2+c=0,c=-3;
∴抛物线的解析式:y=x2-2x-3.
(2)∵抛物线的解析式:y=x2-2x-3=(x-1)2-4=(x+1)(x-3),
∴点C(0,-3)、B(3,0)、E(1,-4);
易知点D(0,1),则有:
OD=1、OB=3、BD=$\sqrt{10}$;
CE=$\sqrt{2}$、BC=3$\sqrt{2}$、BE=2$\sqrt{5}$;
∴$\frac{OD}{CE}=\frac{OB}{BC}=\frac{BD}{BE}$,
∴△BCE∽△BOD.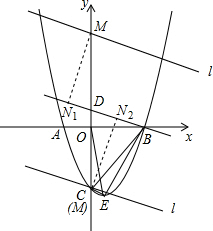 (3)S△BOE=$\frac{1}{2}$×BO×|yE|=$\frac{1}{2}$×3×4=6;
(3)S△BOE=$\frac{1}{2}$×BO×|yE|=$\frac{1}{2}$×3×4=6;
∴S△BDP=$\frac{1}{2}$×BD×h=S△BOE=6,即 h=$\frac{12}{\sqrt{10}}$.
在y轴上取点M,过点M作MN1⊥BD于N1,使得MN1=h=$\frac{12}{\sqrt{10}}$;
在Rt△MN1D中,sin∠MDN1=$\frac{3}{\sqrt{10}}$,且 MN1=$\frac{12}{\sqrt{10}}$;则 MD=$\frac{M{N}_{1}}{sin∠MD{N}_{1}}$=4;
∴点M(0,-3)或(0,5).
过点M作直线l∥MN2,如右图,则 直线l:y=-$\frac{1}{3}$x-3或y=-$\frac{1}{3}$x+5,联立抛物线的解析式有:
$\left\{\begin{array}{l}{y=-\frac{1}{3}x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$或 $\left\{\begin{array}{l}{y=-\frac{1}{3}x+5}\\{y={x}^{2}-2x-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=-3}\end{array}\right.、\left\{\begin{array}{l}{{x}_{2}=\frac{5}{3}}\\{{y}_{2}=-\frac{32}{9}}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{3}=\frac{5+\sqrt{313}}{6}}\\{{y}_{3}=\frac{85-\sqrt{313}}{18}}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{4}=\frac{5-\sqrt{313}}{6}}\\{{y}_{4}=\frac{85+\sqrt{313}}{18}}\end{array}\right.$,
∴当点P的坐标为(0,-3)、$(\frac{5}{3},-\frac{32}{9})、(\frac{5+\sqrt{313}}{6},\frac{85-\sqrt{313}}{18})$、$(\frac{5-\sqrt{313}}{6},\frac{85+\sqrt{313}}{18})$时,△BDP的面积等于△BOE的面积.
点评 该题考查的是涉及到抛物线解析式的确定、相似三角形的判定和性质以及图形面积的解法等重点知识;最后一题中,由于BD不与x轴、y轴垂直,给解答带来了难度,但通过将BD边上的高进行适当转化,得出过点P且与BD平行的直线l的解析式是突破题目的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9π | B. | 16π | C. | 27π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com